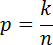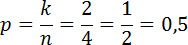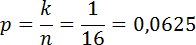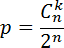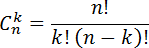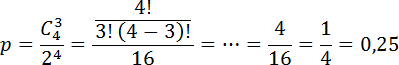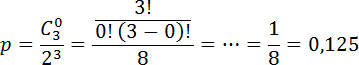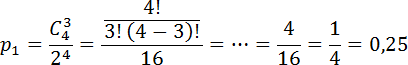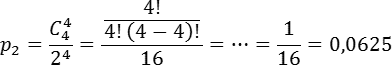Симметричную монету бросают 10 раз найдите вероятность того что орел выпадет
Симметричную монету бросают 10 раз найдите вероятность того что орел выпадет
Задача 1. В случайном эксперименте симметричную монету бросают дважды. Найдите вероятность того, что орел выпадет ровно один раз.
Общее число равновозможных комбинаций может быть четыре:
«орел-орел», «орел-решка», «решка-орел», «решка-решка».
Из них благоприятных исходов по условию задачи два – это «орел-решка» и «решка-орел». Следовательно, искомая вероятность, равна

Задача 2. В случайном эксперименте симметричную монету бросают три раза. Найдите вероятность того, что решка выпадет ровно 2 раза.
1-й способ: Решать эту задачу можно аналогично предыдущей. Всего исходов может быть 8:
Благоприятных исходов по условию задачи 3 – это «орел-решка-решка», «решка-орел-решка», «решка-решка-орел». И искомая вероятность равна

2-й способ. В рамках данной задачи общее число исходов можно определить по формуле

где 


Число благоприятных исходов можно определить по формуле

где 



В итоге получаем искомую вероятность

Второй способ может существенно сократить время на решение подобных задач, особенно когда речь идет о четырех и более подбрасываний монеты. В этом случае перебирать все варианты и не ошибиться становится трудно, и применение указанных формул существенно облегчает задачу.
Задача 3. В случайном эксперименте монету бросают трижды. Найдите вероятность того, что решка выпадет ровно три раза.
В данной задаче имеется только один благоприятный исход из восьми равновероятных исходов:
Следовательно, искомая вероятность равна

Общее число исходов также можно определить по формуле 
Задача 4. Перед началом футбольного матча судья бросает монетку, чтобы определить, какая из команд начнет игру с мячом. Команда «Изумруд» играет три матча с разными командами. Найдите вероятность того, что в этих играх «Изумруд» выиграет жребий ровно один раз.
Будем считать, что выпадение «орла» соответствует началу игры мячом команды «Изумруд». Тогда задача сводится к определению вероятности выпадения «орла» ровно один раз из трех бросаний монеты.
Всего исходов 8 (см. предыдущие задачи). Из них «орел» выпадет ровно один раз в 

Симметричную монету бросают 10 раз найдите вероятность того что орел выпадет
В случайном эксперименте симметричную монету бросают трижды. Найдите вероятность того, что орел выпадет ровно два раза.
Обозначим выпадение орла буквой О, а выпадение решки буквой Р. Возможных восемь исходов:
OOO, OОР, ОРО, ОРР, РОО, РОР, РРО, РРР
Из них благоприятными являются OОР, ОРО и РОО. Поэтому искомая вероятность равна то есть 0,375. (Этот подход затруднителен в случае большого числа бросаний монетки.)
Приведем другое решение.
Каждое бросание с равной вероятностью может дать орел или решку, поэтому для трех бросаний равновозможны различных вариантов. Орел выпадает ровно два раза в трех случаях: орел-решка-орел, решка-орел-орел, орел-орел-решка. Поэтому вероятность этого события
Приведем решение, основанное на комбинаторных формулах.
Общее количество различных вариантов описывается формулой для размещений с повторениями: Количество способов получить ровно три орла дается перестановками с повторениями
Искомая вероятность равна отношению благоприятных случаев ко всем возможным:
Приведем решение, использующее теоремы о вероятностях.
Возможны три варианта: орел-орел-решка, орел-решка-орел, решка-орел-орел. Эти события несовместные, вероятность их суммы равна сумме вероятностей этих событий:
Вероятность выпадения монетки одной стороной и дважды — другой стороной равна 0,5·0,5·0,5 = 0,125. Выбрать из этих «трех» сторон два орла можно способами. Следовательно, искомая вероятность равна 0,375.
Примечание. Последнее рассуждение — не что иное, как вывод формулы Бернулли для нашего случая. В общем случае, если проводится n испытаний, в каждом из которых некоторое событие наступает в вероятностью p, то вероятность наступления этого события ровно k раз дается формулой
Монету бросают 10 раз какова вероятность
Кстати, сразу упомяну, что в контексте подобных задач не существенно, написать «бросают 3 монеты» или «бросают монету 3 раза», результат (в смысле вычисления вероятности) будет один и тот же (так как результаты бросков независимы друг от друга).
Для задач о подбрасывании монеты существуют два основных метода решения, один – по формуле классической вероятности (фактически переборный метод, доступный даже школьникам), а также его более сложный вариант с использованием комбинаторики, второй – по формуле Бернулли (на мой взгляд он даже легче первого, нужно только запомнить формулу). Рекомендую по порядку прочитать про оба метода, и потом выбирать при решении подходящий.
1. Классическое определение вероятности
Пример 1. В случайном эксперименте симметричную монету бросают дважды. Найдите вероятность того, что орел выпадет ровно один раз.
Пример 2. Дважды бросают симметричную монету. Найти вероятность того, что оба раза выпала одна сторона.
Как видим, все довольно просто. Перейдем к чуть более сложной задаче.
Пример 3. В случайном эксперименте симметричную монету бросают трижды. Найдите вероятность того, что орел выпадет ровно два раза.
Взяли разгон и переходим к 4 монетам.
Пример 4. Монету бросают 4 раза. Найти вероятность того, что герб выпадет от 2 до 3 раз.
Думаю, к этому времени вы уже поняли суть метода и сможете сами решить задачи, где бросаются 2-3-4 монеты и орел не выпадает ни разу, или решка ровно один раз и т.п.
2. Комбинаторика + классическая вероятность
Надо заметить, что если действовать исключительно переборным методом (как это делалось выше), с ростом числа монет быстро растет число комбинаций (для 5 монет – 32, для 6 монет – 64 и так далее), так что и вероятность ошибиться при выписывании исходов велика, метод решения теряет свою простоту и привлекательность.
Один из способов решения этой проблемы – остаться в рамках формулы классической вероятности, но использовать комбинаторные методы (см. формулы комбинаторики тут) для подсчета числа исходов. Поясню на примере последней задачи, решив ее другим способом.
Пример 4. Монету бросают 4 раза. Найти вероятность того, что герб выпадет от 2 до 3 раз.
Конечно, этот подход кажется сложнее из-за более формального математического описания решения, но гораздо легче масштабируется.
Например, если рассмотреть подобную задачу:
Пример 5. Монету бросают 8 раз. Найти вероятность того, что герб выпадет ровно 4 раза
Ради полноты изложения приведу еще пример задачи, решаемой подобным образом (но если хотите, можете сразу переходить к более простому способу 3).
Пример 6. Монету подбрасывают 6 раз. Найти вероятность того, что гербы выпадут два раза и только подряд, а в остальные разы будут только решки.
Способ 3. Формула Бернулли
А теперь все задачи решаются проще простого, вот глядите!
Пример 1. В случайном эксперименте симметричную монету бросают дважды. Найдите вероятность того, что орел выпадет ровно один раз.
Пример 4. Монету бросают 4 раза. Найти вероятность того, что герб выпадет от 2 до 3 раз.
Пример 7. В случайном эксперименте симметричную монету бросают трижды. Найдите вероятность того, что орел не выпадет ни разу.
Пример 8. Пусть бросают 8 монет. Найти вероятность того, что орел не менее 7 раз.
Таким образом, используя одну простейшую формулу, можно решать множество задач, причем неважно, 3 монеты бросается, или 30, сложность расчетов примерно одинакова. Но, если число бросков становится очень большим, удобнее использовать приближенные формулы Муавра-Лапласа, о которых можно узнать здесь.
Полезные ссылки
Решебник по вероятности
А здесь вы найдете более 200 задач о бросании монет с полными решениями (вводите часть текста для поиска своей задачи):
Монета брошена 10 раз. Найти вероятность того, что герб выпадет: а) от 4-х до 6-ти раз; б) хотя бы один раз.
Решение. События выпадения герба при многократном бросании монеты являются независимыми. В каждом испытании герб, так же, как и надпись, выпадает с вероятностью р = 0,5. Таким образом, задача относит-ся к схеме и формуле Бернулли. Для случая а) искомая вероятность вычисле-ния по формуле (2.4), а для случая б) – по формуле (2.3). С помощью этих формул, с учетом того, что р = 0,5 и q = 0,5 получим:
б) р10(хотя бы один раз) = 1 – q 10 = 1 – 1/1024=1023/1024.
нПОЕФХ ВТПУБАФ 10 ТБЪ. оБКДЙФЕ ЧЕТПСФОПУФШ ФПЗП, ЮФП ОЙ ТБЪХ ОЕ ЧЩРБДХФ ДЧБ ПТМБ РПДТСД.
тЕЫЕОЙЕ
рЕТЧЩК УРПУПВ. еУМЙ ПТМПЧ ОЕФ ЧПЧУЕ, ФП ФБЛБС РПУМЕДПЧБФЕМШОПУФШ УПУФПЙФ ЙЪ ДЕУСФЙ ТЕЫЕЛ Й ЧУЕЗП ПДОБ. еУМЙ ПТЕМ ПДЙО, ФП ФБЛЙИ ЛПНВЙОБГЙК 10 (ПТЕМ УФПЙФ ОБ МАВПН ЙЪ 10 НЕУФ). еУМЙ ПТМПЧ ДЧБ, ФП ЛПНВЙОБГЙК (НЩ УЮЙФБЕН ЛПМЙЮЕУФЧП ЧБТЙБОФПЧ ТБУУФБЧЙФШ 2 ПТМБ РП ПДОПНХ НЕЦДХ 8 ТЕЫЛБНЙ ЙМЙ РП ЛТБСН). й ФБЛ ДБМЕЕ. еУМЙ ПТМПЧ k, ФП ЛПНВЙОБГЙК (ЮЙУМП ЧБТЙБОФПЧ ТБУУФБЧЙФШ ПТМПЧ Ч 11 – k НЕУФ НЕЦДХ ТЕЫЛБНЙ Й РП ЛТБСН).
ъОБЮЙФ, ПВЭЕЕ ЮЙУМП ЛПНВЙОБГЙК ТБЧОП
уМЕДПЧБФЕМШОП, ЙУЛПНБС ЧЕТПСФОПУФШ ЕУФШ 144 : 2 10 = 9 /64.
пФЧЕФ
йУФПЮОЙЛЙ Й РТЕГЕДЕОФЩ ЙУРПМШЪПЧБОЙС
| ПМЙНРЙБДБ | |
| оБЪЧБОЙЕ | ъБПЮОБС ПМЙНРЙБДБ РП ФЕПТЙЙ ЧЕТПСФОПУФЕК Й УФБФЙУФЙЛЕ |
| ЗПД | |
| дБФБ | 2009 |
| ЪБДБЮБ | |
| оПНЕТ | 13 |
Задачи B6 с монетами
Задачи на подбрасывание монет считаются довольно сложными. И перед тем как решать их, требуется небольшое пояснение. Задумайтесь, любая задача по теории вероятностей в итоге сводится к стандартной формуле:
где искомая вероятность, число устраивающих нас событий, общее число возможных событий.
Большинство задач B6 решаются по этой формуле буквально в одну строчку — достаточно прочитать условие. Но в случае с подбрасыванием монет эта формула бесполезна, поскольку из текста таких задач вообще не понятно, чему равны числа В этом и состоит вся сложность.
Тем не менее, существует как минимум два принципиально различных метода решения:
Для решения задачи B6 надо знать оба метода. К сожалению, в школах изучают только первый. Не будем повторять школьных ошибок. Итак, поехали!
Метод перебора комбинаций
Этот метод еще называется «решение напролом». Состоит из трех шагов:
К сожалению, этот способ работает лишь для малого количества бросков. Потому что с каждым новым броском число комбинаций удваивается. Например, для 2 монет придется выписать всего 4 комбинации. Для 3 монет их уже 8, а для 4 — 16, и вероятность ошибки приближается к 100%. Взгляните на примеры — и сами все поймете:
Задача. В случайном эксперименте симметричную монету бросают 2 раза. Найдите вероятность того, что орлов и решек выпадет одинаковое количество.
Итак, монету бросают два раза. Выпишем все возможные комбинации (O — орел, P — решка):
Итого варианта. Теперь выпишем те варианты, которые подходят по условию задачи:
Таких вариантов оказалось Находим вероятность:
Задача. Монету бросают четыре раза. Найдите вероятность того, что решка не выпадет ни разу.
Снова выписываем все возможные комбинации орлов и решек:
OOOO OOOP OOPO OOPP OPOO OPOP OPPO OPPP
POOO POOP POPO POPP PPOO PPOP PPPO PPPP
Всего получилось вариантов. Вроде, ничего не забыл. Из этих вариантов нас устраивает лишь комбинация «OOOO», в которой вообще нет решек. Следовательно, Осталось найти вероятность:
Как видите, в последней задаче пришлось выписывать 16 вариантов. Вы уверены, что сможете выписать их без единой ошибки? Лично я — не уверен. Поэтому давайте рассмотрим второй способ решения.
Специальная формула вероятности
Итак, в задачах с монетами есть собственная формула вероятности. Она настолько простая и важная, что я решил оформить ее в виде теоремы. Взгляните:
Теорема. Пусть монету бросают Тогда вероятность того, что орел выпадет ровно можно найти по формуле:
Где Cn k — число сочетаний которое считается по формуле:
Таким образом, для решения задачи с монетами нужны два числа: число бросков и число орлов. Чаще всего эти числа даны прямо в тексте задачи. Более того, не имеет значения, что именно считать: решки или орлы. Ответ получится один и тот же.
На первый взгляд, теорема кажется слишком громоздкой. Но стоит чуть-чуть потренироваться — и вам уже не захочется возвращаться к стандартному алгоритму, описанному выше.
Задача. Монету бросают четыре раза. Найдите вероятность того, что орел выпадет ровно три раза.
По условию задачи, всего бросков было Требуемое число орлов: Подставляем в формулу:
С тем же успехом можно считать число решек: Ответ будет таким же.
Задача. Монету бросают три раза. Найдите вероятность того, что решка не выпадет ни разу.
Снова выписываем числа Поскольку монету бросают 3 раза, А поскольку решек быть не должно, Осталось подставить числа в формулу:
Напомню, что 0! = 1 по определению. Поэтому C 3 0 = 1.
Задача. В случайном эксперименте симметричную монету бросают 4 раза. Найдите вероятность того, что орел выпадет больше раз, чем решка.
Чтобы орлов было больше, чем решек, они должны выпасть либо 3 раза (тогда решек будет 1), либо 4 (тогда решек вообще не будет). Найдем вероятность каждого из этих событий.
Пусть вероятность того, что орел выпадет 3 раза. Тогда Имеем:
Теперь найдем вероятность того, что орел выпадет все 4 раза. В этом случае Имеем:
Чтобы получить ответ, осталось сложить вероятности p 1 и p 2. Помните: складывать вероятности можно только для взаимоисключающих событий. Имеем:
p = p 1 + p 2 = 0,25 + 0,0625 = 0,3125
Задание 10 ЕГЭ по математике. Теория вероятностей. Повышенный уровень сложности
В 2022 году в варианты ЕГЭ по математике добавились новые задачи по теории вероятностей. По сравнению с теми, которые раньше были в варианте, это повышенный уровень сложности.
Мы разберем задачу №10 из Демоверсии ЕГЭ-2022, задания из Методических рекомендаций ФИПИ для учителей и аналогичные им.
1. Демо-версия ЕГЭ-2022
Симметричную игральную кость бросили 3 раза. Известно, что в сумме выпало
6 очков. Какова вероятность события «хотя бы раз выпало 3 очка»?
Выпишем возможные исходы как тройки чисел так, чтобы в сумме получилось 6.
Всего 10 возможных исходов. Благоприятные исходы помечены красным цветом, их 6.
По определению вероятности получаем
2. Игральный кубик бросают дважды. Известно, что в сумме выпало 8 очков. Найдите вероятность того, что во второй раз выпало 3 очка.
Выпишем возможные варианты получения 8 очков в сумме:
Подходит только вариант 5; 3. Вероятность этого события равна 1 : 5 = 0,2 (один случай из 5 возможных).
3. В ящике 4 красных и 2 синих фломастера. Фломастеры вытаскивают по очереди в случайном порядке. Какова вероятность того, что первый раз синий фломастер появится третьим по счету?
Благоприятными будут следующие исходы:
Первый раз – вытащили красный фломастер,
И второй раз – красный,
А третий раз – синий.
Вероятность вытащить красный фломастер (которых в ящике 4) равна
После этого в ящике остается 5 фломастеров, из них 3 красных, вероятность вытащить красный равна
Наконец, когда осталось 4 фломастера и из них 2 синих, вероятность вытащить синий равна
Вероятность события <красный – красный – синий >равна произведению этих вероятностей, то есть
4. В коробке 10 синих, 9 красных и 6 зеленых фломастеров. Случайным образом выбирают 2 фломастера. Какова вероятность того, что окажутся выбраны один синий и один красный фломастер?
Всего в коробке 25 фломастеров.
В условии не сказано, какой из фломастеров вытащили первым – красный или синий.
Предположим, что первым вытащили красный фломастер. Вероятность этого в коробке остается 24 фломастера, и вероятность вытащить вторым синий равна Вероятность того, что первым вытащили красный, а вторым синий, равна
А если первым вытащили синий фломастер? Вероятность этого события равна Вероятность после этого вытащить красный равна вероятность того, что синий и красный вытащили один за другим, равна
Значит, вероятность вытащить первым красный, вторым синий или первым синий, вторым красный равна
А если их доставали из коробки не один за другим, а одновременно? Вероятность остается такой же: 0,3. Потому что она не зависит от того, вытащили мы фломастеры один за другим, или с интервалом в 2 секунды, или с интервалом в 0,5 секунды… или одновременно!
Ответ: 0,3.
5. При подозрение на наличие некоторого заболевания пациента отправляют на ПЦР-тест. Если заболевание действительно есть, то тест подтверждает его в 86 % случаев. Если заболевания нет, то тест выявляет отсутствие заболевания в среднем в 94% случаев.
Известно, что в среднем тест оказывается положительным у 10% пациентов, направленных на тестирование. При обследовании некоторого пациента врач направил его на ПЦР-тест, который оказался положительным. Какова вероятность того, что пациент действительно имеет это заболевание?
Пациент приходит к врачу и делает ПЦР-тест. Он может быть болен этим заболеванием – с вероятностью х. Тогда с вероятностью 1 – х он этим заболеванием не болен.
Анализ пациента может быть положительным по двум причинам:
а) пациент болеет заболеванием, которое нельзя называть, его анализ верен; событие А,
б) пациент не болен этим заболеванием, его анализ ложно-положительный, событие В.
Это несовместные события, и вероятность их суммы равна сумме вероятностей этих событий.
Мы составили уравнение, решив которое, найдем вероятность x.
Нам же нужно найти вероятность z того, что пациент, ПЦР-тест которого положителен, действительно имеет это заболевание. Вероятность этого события равна (пациент болен и ПЦР-тест выявил заболевание, произведение событий). С другой стороны, эта вероятность равна (у пациента положительный результат ПЦР-теста, и при выполнении этого условия он действительно болен).
Вероятность того, что пациент с положительным результатом ПЦР-теста действительно болен, меньше половины!
Кстати, это реальная проблема для диагностики в медицине, то есть в задаче отражена вполне жизненная ситуация.
6. Телефон передает sms-сообщение. В случае неудачи телефон делает следующую попытку. Вероятность того, что сообщение удастся передать без ошибок в каждой следующей попытке, равна 0,4. Найдите вероятность того, что для передачи сообщения потребуется не больше 2 попыток.
Решение:
Здесь все просто. Либо сообщение удалось передать с первой попытки, либо со второй.
Вероятность того, что сообщение удалось передать с первой попытки, равна 0,4.
С вероятностью 0,6 с первой попытки передать не получилось. Если при этом получилось со второй, то вероятность этого события равна
Значит, вероятность того, что для передачи сообщения потребовалось не более 2 попыток, равна
7. Симметричную монету бросают 10 раз. Во сколько раз вероятность события «выпадет ровно 5 орлов» больше вероятности события «выпадет ровно 4 орла»?
А это более сложная задача. Можно, как и в предыдущих, пользоваться определением вероятности и понятиями суммы и произведения событий. А можно применить формулу Бернулли.
Формула Бернулли:
– Вероятность того, что в n независимых испытаниях некоторое случайное событие A наступит ровно m раз, равна:
p – вероятность появления события A в каждом испытании;
– вероятность появления события A в каждом испытании
Коэффициент часто называют биномиальным коэффициентом.
О том, что это такое, расскажем с следующих статьях на нашем сайте. Чтобы не пропустить – подписывайтесь на нашу рассылку.
А пока скажем просто, как их вычислять.
Нет, это не заклинание. Не нужно громко кричать: Эн. Поделить на эм! И на эн минус эм! То, что вы видите в формуле, – это не восклицательные знаки. Это факториалы. На самом деле все просто: n! (читается: эн факториал) – это произведение натуральных чисел от 1 до n. Например,
Пусть вероятность выпадения орла при одном броске монеты равна вероятность решки тоже Давайте посчитаем вероятность того, что из 10 бросков монеты выпадет ровно 5 орлов.
Вероятность выпадения ровно 4 орлов равна
Найдем, во сколько раз больше, чем
8. Стрелок стреляет по пяти одинаковым мишеням. На каждую мишень дается не более двух выстрелов, и известно, что вероятность поразить мишень каждым отдельным выстрелом равна 0,6. Во сколько раз вероятность события «стрелок поразит ровно 5 мишеней» больше вероятности события «стрелок поразит ровно 4 мишени»?
Стрелок поражает мишень с первого или со второго выстрела;
Вероятность поразить мишень равна
Вероятность поразить 5 мишеней из 5 равна
Вероятность поразить 4 мишени из 5 находим по формуле Бернулли:
9. Стрелок стреляет по пяти одинаковым мишеням. На каждую мишень дается не более двух выстрелов, и известно, что вероятность поразить мишень каждым выстрелом равна 0,5. Во сколько раз вероятность события «стрелок поразит ровно 3 мишени» больше вероятности события «стрелок поразит ровно 2 мишени»?
Решение:
Найдем вероятность поразить одну мишень – с первого или со второго выстрела.
С вероятностью стрелок поражает мишень первым выстрелом (и больше по ней не стреляет).
Найдем вероятность того, что стрелок поразит мишень вторым выстрелом. Она равна так как с вероятностью он промахнулся в первый раз и с вероятностью второй выстрел был удачным.
Значит, вероятность поразить одну мишень первым или вторым выстрелом равна
Теперь нам на помощь придет формула Бернулли.
Найдем вероятность того, что стрелок поразит ровно 3 мишени из 5.
Вероятность поразить ровно 2 мишени из пяти
10. Стрелок в тире стреляет по мишени. Известно, что он попадает в цель с вероятностью 0,3 при каждом отдельном выстреле. Какое наименьшее количество патронов нужно дать этому стрелку, чтобы вероятность поражения цели была не менее 0,6?
Вероятность промаха при одном выстреле равна 1 – 0,3 = 0,7.
Если то – не подходит;
Для условие выполнено,
11. Игральную кость бросают до тех пор, пока сумма всех выпавших очков не превысит число 3. Какова вероятность того, что для этого потребуется ровно 3 броска? Ответ округлите до сотых.
Кажется, что задача сложная (на самом деле нет).
Давайте подумаем: как получилось, что ровно за 3 броска игральной кости сумма выпавших очков оказалась больше трех? Из этого следует, что за 2 броска сумма выпавших очков была меньше 3 или равна 3.
Если за 2 броска сумма выпавших очков была меньше 3, значит, она была равна 2, то есть первый раз выпала единица и второй раз тоже единица. Вероятность этого события равна
Сколько же очков в этом случае должен дать третий бросок? Очевидно, что подойдет 2, 3, 4, 5, 6 – все, кроме 1. Вероятность того, что при третьем броске выпадет число очков, не равное единице, равна
Значит, вероятность того, что при первых двух бросках выпали единицы, а при третьем – не единица, равна
Нам подойдет также случай, когда сумма очков за первые 2 броска равна 3. Это значит, что выпали 2 и 1 или 1 и 2, то есть 2 благоприятных исхода из 36 возможных. Вероятность этого события равна
При этом нам все равно, что выпадет при третьем броске: очевидно, что сумма очков при трех бросках будет больше трех.
Вот еще одна задача из Демо-версии ЕГЭ-2022:
12. В городе 48% взрослого населения – мужчины. Пенсионеры составляют 12,6% взрослого населения, причём доля пенсионеров среди женщин равна 15%. Для социологического опроса выбран случайным образом мужчина, проживающий в этом городе. Найдите вероятность события «выбранный мужчина является пенсионером».
Решение:
Пусть N – численность взрослого населения в городе (мужчин и женщин).
Количество взрослых мужчин в городе: 0,48N
Количество женщин в городе: 0,52N
Из них 0,15 * 0,52N = 0,078N женщин-пенсионеров,
Всего пенсионеров 0,126N,
Тогда количество мужчин-пенсионеров равно 0,126N – 0,078N = 0,048N.
Вероятность для случайно выбранного мужчины оказаться пенсионером равна отношению числа мужчин-пенсионеров к числу мужчин в городе, то есть 0,048 N : 0,48N = 0,1.
Ответ. 0,1.
Мы разобрали все доступные типы заданий №10 из вариантов ЕГЭ-2022. Раздел будет дополняться решениями новых задач– как только они появятся в Банке заданий ФИПИ.