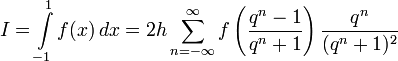Технология самокиша что это

Метод Самокиша

Рассмотрим определённый интеграл с особенностями на концах промежутка [-1;1]

Пусть требуется вычислить — оба конца особые. Метод заключается в отбрасывании концов на бесконечность, заменой переменных:

, тогда интеграл принимает следующий вид:

Интеграл берется по формуле трапеций. Пусть ,где , m — количество промежутков деления, тогда :

Суммирование заканчивается, когда остаток ряда меньше заданного ε.

Библиография

Полезное

Смотреть что такое «Метод Самокиша» в других словарях:

Метод самокиша — (Формула Стенжера) метод численного интегрирования интегралов с особенностями. Рассмотрим определённый интеграл с особенностями на концах промежутка [ 1;1] Пусть требуется вычислить оба конца особые. Метод заключается в отбрасывании концов на… … Википедия

Численное интегрирование — (историческое название: (численная) квадратура) вычисление значения определённого интеграла (как правило, приближённое). Под численным интегрированием понимают набор численных методов отыскания значения определённого интеграла. Численное… … Википедия

Квадратурные формулы — Определённый интеграл как площадь фигуры Численное интегрирование (историческое название: квадратура) вычисление значения определённого интеграла (как правило, приближённое), основанное на том, что величина интеграла численно равна площади… … Википедия

Квадратурная формула — Определённый интеграл как площадь фигуры Численное интегрирование (историческое название: квадратура) вычисление значения определённого интеграла (как правило, приближённое), основанное на том, что величина интеграла численно равна площади… … Википедия

Прямоугольников формула — Определённый интеграл как площадь фигуры Численное интегрирование (историческое название: квадратура) вычисление значения определённого интеграла (как правило, приближённое), основанное на том, что величина интеграла численно равна площади… … Википедия

Формула прямоугольников — Определённый интеграл как площадь фигуры Численное интегрирование (историческое название: квадратура) вычисление значения определённого интеграла (как правило, приближённое), основанное на том, что величина интеграла численно равна площади… … Википедия

Формула трапеций — Определённый интеграл как площадь фигуры Численное интегрирование (историческое название: квадратура) вычисление значения определённого интеграла (как правило, приближённое), основанное на том, что величина интеграла численно равна площади… … Википедия

Несобственный интеграл — Определённый интеграл называется несобственным, если выполняется, по крайней мере, одно из следующих условий: Предел a или b (или оба предела) являются бесконечными; Функция f(x) имеет одну или несколько точек разрыва внутри отрезка [a, b].… … Википедия

Несобственные интегралы — Содержание 1 Определение 2 Критерий Коши 3 Абсолютная сходимость 4 См. также // … Википедия

Чепелик, Виктор Васильевич — Виктор Васильевич Чепелик Чепелик В. В., 1950 е годы Основные сведения Гражданство … Википедия

Источник

Метод самокиша

Рассмотрим определённый интеграл с особенностями на концах промежутка [-1;1]

Пусть требуется вычислить — оба конца особые. Метод заключается в отбрасывании концов на бесконечность, заменой переменных:

, тогда интеграл принимает следующий вид:

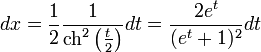
Суммирование заканчивается, когда остаток ряда меньше заданного ε.

Полезное

Смотреть что такое «Метод самокиша» в других словарях:

Метод Самокиша — (Формула Стенжера) метод численного интегрирования интегралов с особенностями. Рассмотрим определённый интеграл с особенностями на концах промежутка [ 1;1] Пусть требуется вычислить оба конца особые. Метод заключается в отбрасывании… … Википедия

Численное интегрирование — (историческое название: (численная) квадратура) вычисление значения определённого интеграла (как правило, приближённое). Под численным интегрированием понимают набор численных методов отыскания значения определённого интеграла. Численное… … Википедия

Квадратурные формулы — Определённый интеграл как площадь фигуры Численное интегрирование (историческое название: квадратура) вычисление значения определённого интеграла (как правило, приближённое), основанное на том, что величина интеграла численно равна площади… … Википедия

Квадратурная формула — Определённый интеграл как площадь фигуры Численное интегрирование (историческое название: квадратура) вычисление значения определённого интеграла (как правило, приближённое), основанное на том, что величина интеграла численно равна площади… … Википедия

Прямоугольников формула — Определённый интеграл как площадь фигуры Численное интегрирование (историческое название: квадратура) вычисление значения определённого интеграла (как правило, приближённое), основанное на том, что величина интеграла численно равна площади… … Википедия

Формула прямоугольников — Определённый интеграл как площадь фигуры Численное интегрирование (историческое название: квадратура) вычисление значения определённого интеграла (как правило, приближённое), основанное на том, что величина интеграла численно равна площади… … Википедия

Формула трапеций — Определённый интеграл как площадь фигуры Численное интегрирование (историческое название: квадратура) вычисление значения определённого интеграла (как правило, приближённое), основанное на том, что величина интеграла численно равна площади… … Википедия

Несобственный интеграл — Определённый интеграл называется несобственным, если выполняется, по крайней мере, одно из следующих условий: Предел a или b (или оба предела) являются бесконечными; Функция f(x) имеет одну или несколько точек разрыва внутри отрезка [a, b].… … Википедия

Несобственные интегралы — Содержание 1 Определение 2 Критерий Коши 3 Абсолютная сходимость 4 См. также // … Википедия

Чепелик, Виктор Васильевич — Виктор Васильевич Чепелик Чепелик В. В., 1950 е годы Основные сведения Гражданство … Википедия

Источник