Тавтология в математике что это

Тавтология (логика)

Содержание

История [ править ]

В 1800 году Иммануил Кант написал в своей книге « Логика» :

Идентичность понятий в аналитических суждениях может быть либо явным ( explicita ) или без явного ( implicita ). В первом случае аналитические предложения тавтологичны.

В 1884 году Готтлоб Фреге в своей книге «Grundlagen» предложил, что истина аналитична именно тогда, когда ее можно вывести с помощью логики. Однако он проводил различие между аналитическими истинами (т. Е. Истинами, основанными только на значениях их терминов) и тавтологиями (т. Е. Утверждениями, лишенными содержания).

Все, что является утверждением логики, должно быть в том или ином смысле похоже на тавтологию. Это должно быть что-то, имеющее какое-то особое качество, которое я не знаю, как определить, что принадлежит логическим предложениям, но не другим.

Здесь логическое предложение относится к предложению, которое можно доказать с помощью законов логики.

Фон [ править ]

Определение и примеры [ править ]

Проверка тавтологий [ править ]

Например, рассмотрим формулу

Также возможно определить дедуктивную систему (т. Е. Систему доказательств) для логики высказываний как более простой вариант дедуктивных систем, используемых для логики первого порядка (об одной такой системе см. Клини 1967, раздел 1.9). Доказательство тавтологии в соответствующей системе дедукции может быть намного короче, чем полная таблица истинности (формула с n пропозициональными переменными требует таблицы истинности с 2 n строками, которая быстро становится невыполнимой при увеличении n ). Системы доказательств также требуются для изучения интуиционистской логики высказываний, в которой метод таблиц истинности не может быть использован, поскольку не предполагается закон исключенного третьего.

Тавтологический смысл [ править ]

Замена [ править ]

Из правила подстановки следует, что предложение

Семантическая полнота и правильность [ править ]

Эффективная проверка и проблема логической выполнимости [ править ]

Тавтологии и валидности в логике первого порядка [ править ]

Не все логические обоснования являются тавтологиями в логике первого порядка. Например, предложение

На естественном языке [ править ]

Источник

СОДЕРЖАНИЕ

История

В 1800 году Иммануил Кант написал в своей книге « Логика» :

Идентичность понятий в аналитических суждениях может быть либо явным ( explicita ) или без явного ( implicita ). В первом случае аналитические предложения тавтологичны.

В 1884 году Готтлоб Фреге предложил в своей книге «Grundlagen», что истина является аналитической именно тогда, когда ее можно вывести с помощью логики. Однако он проводил различие между аналитическими истинами (т. Е. Истинами, основанными только на значениях их терминов) и тавтологиями (т. Е. Утверждениями, лишенными содержания).

Все, что является утверждением логики, должно быть в том или ином смысле похоже на тавтологию. Это должно быть что-то с каким-то особым качеством, которое я не знаю, как определить, что принадлежит логическим предложениям, но не другим.

Здесь логическое предложение относится к предложению, которое можно доказать с помощью законов логики.

Определение и примеры

Проверка тавтологий

Например, рассмотрим формулу

Также возможно определить дедуктивную систему (т. Е. Систему доказательств) для логики высказываний как более простой вариант дедуктивных систем, используемых для логики первого порядка (об одной такой системе см. Клини 1967, раздел 1.9). Доказательство тавтологии в соответствующей системе дедукции может быть намного короче, чем полная таблица истинности (формула с n пропозициональными переменными требует таблицы истинности с 2 n строками, которая быстро становится невыполнимой при увеличении n ). Системы доказательства также требуются для изучения интуиционистской логики высказываний, в которой метод таблиц истинности не может быть использован, потому что не предполагается закон исключенного третьего.

Тавтологический подтекст

Замена

Из правила подстановки следует, что предложение

Семантическая полнота и обоснованность

Эффективная проверка и проблема логической выполнимости

Тавтологии и валидности в логике первого порядка

Не все логические обоснования являются тавтологиями в логике первого порядка. Например, предложение

Источник

1. Высказывания, формулы, тавтологии

Определение. Высказыванием называется утверждение, которое является истинным или ложным (но не одновременно).

То есть, чтобы выяснить, является ли некоторое предложение высказыванием, нужно сначала убедиться, что это утверждение, а затем установить, истинно оно или ложно.

Пример. “Москва – столица России” – истинное высказывание.

“5 –четное число” – ложное высказывание.

“” – не высказывание (неизвестно, какие значения принимает ).

“Студент второго курса” не высказывание (не является утверждением).

Высказывания бывают элементарные и составные.

Элементарные высказывания не могут быть выражены через другие высказывания. Составные высказывания можно выразить с помощью элементарных высказываний.

Пример. “Число 22 четное” – элементарное высказывание.

“Число 22 четное и делится на 11” – составное высказывание.

Высказывания обозначают заглавными буквами латинского алфавита: , , ,… Эти буквы называют логическими Атомами.

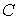
При фиксированном множестве букв Интерпретацией называется функция , которая отображает множество во множество истинностных (логических) значений , то есть .

Истинностные значения истина и ложь сокращенно обозначаются и, л или T, F, или 1,0. Мы будем использовать обозначения 1 и 0. В определенной интерпретации буквы принимают значения 1 или 0.

К высказываниям и буквам можно применять известные из курса дискретной математики логические связки или логические операции. При этом получаются Формулы (формы). Формулы становятся высказываниями при подстановке всех значений букв.

Таблицы истинности основных логических операций.

Более строго формула определяется так.

Определение. 1) Всякая буква есть формула.

2) Если , — формулы, то формулами являются также , , , , .

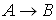
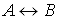
3) Символ является формулой тогда и только тогда, когда это следует из 1) и 2).

В классической логике формулы принято заключать в круглые скобки, но в мы этого делать не будем. Для всякой формулы можно построить таблицу истинности.

Значение формулы 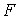в заданной интерпретации обозначают (или , или ).

Часть формулы, которая сама является формулой, называется Подформулой данной формулы.

Определение. Формула называется Тавтологией, если она принимает только истинные значения при любых значениях букв.

Другими словами, тавтология – это тождественно истинная формула.

Установить, является ли формула тавтологией, можно:

– по таблице истинности,

– используя свойства логических операций.

Из курса дискретной математики известны основные логические эквивалентности (свойства логических операций), которые являются примерами тавтологий.

1. Коммутативность: , .

, .

, .

4. Идемпотентность: , .

5. Закон двойного отрицания: .

6. Закон исключения третьего: .

7. Закон противоречия: .

8. Законы де Моргана:

, .

9. Свойства операций с логическими константами:

, , , .

Здесь , и – любые буквы.

Примеры. 1. Доказать, что формула 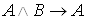является тавтологией.

Доказательство. Допустим, что при некоторых значениях букв (то есть в некоторой интерпретации)

Приходим к противоречию, которое доказывает, что исходная формула – тавтология.

2. Доказать, что формула является тавтологией.

Доказательство. Эквиваленция истинна, если левая и правая части принимают одинаковые значения на некотором наборе значений букв.

Допустим, что при некоторых значениях букв

Следовательно, исходная формула – тавтология.

3. Доказать, что формула является тавтологией.

Доказательство. Допустим, что при некоторых значениях букв

Следовательно, исходная формула – тавтология.

Таким образом, тождественную истинность импликации удобно доказывать от противного, а тождественную истинность эквиваленции установлением равенства значений левой и правой части.

Теорема. Пусть формулы и – тавтологии. Тогда формула – тавтология.

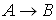
Доказательство. Пусть , , …, – буквы в формулах и . В теории булевых функций было доказано, что все булевы функции, а, следовательно, и формулы, можно считать зависящими от одного и того же количества букв. Рассмотрим некоторый набор значений , , …, , где , . Подставим данный набор значений в формулы и вместо соответствующих букв. Формулы являются тавтологиями по условию теоремы, следовательно, и . По таблице истинности импликации получаем, что . Поскольку набор значений , , …, был произволен, формула – тавтология, что и требовалось доказать.

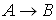
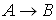
Теорема. Пусть формула – тавтология, , , …, – буквы в формуле , , , …, – любые формулы. Тогда новая формула – тавтология.

Доказательство аналогично доказательству предыдущей теоремы.

Источник

ТАВТОЛОГИЯ

— формула языка исчисления высказываний, принимающая истинностное значение листина

Смотреть что такое «ТАВТОЛОГИЯ» в других словарях:

тавтология — тавтология … Орфографический словарь-справочник

Тавтология — (греческое tautologéō «говорю то же самое») термин античной стилистики, обозначающий повторение однозначных или тех же слов. Античная стилистика подводит многословие речи под три понятия: периссология накопление одинаковых по значению слов, напр … Литературная энциклопедия

ТАВТОЛОГИЯ — (греч., от tauto то же, и logos слово). Выражение одной и той же идеи различными однозначащими словами; ненужное повторение в других выражения сказанного уже раньше. Словарь иностранных слов, вошедших в состав русского языка. Чудинов А.Н., 1910.… … Словарь иностранных слов русского языка

ТАВТОЛОГИЯ — в обычном языке: повторение того, что уже было сказано. Напр.: «Стол есть стол». Т. бессодержательна и пуста, она не несет никакой информации, и от нее стремятся избавиться как от ненужного балласта, загромождающего речь и затрудняющего общение.… … Философская энциклопедия

Тавтология — Тавтология: Тавтология (риторика) (от др. греч. ταυτολογία) риторическая фигура, представляющая собой повторение одних и тех же или близких по смыслу слов. Тавтология (логика) тождественно истинное высказывание, инвариантное… … Википедия

тавтология — повторение, ошибка, масло масляное, высказывание, круг, суждение Словарь русских синонимов. тавтология масло масляное (разг.) Словарь синонимов русского языка. Практический справочник. М.: Русский язык. З. Е. Александрова. 2011 … Словарь синонимов

Тавтология — Тавтология ♦ Tautologie Суждение, которое всегда истинно – либо потому, что предикат лишь повторяет субъект («Бог есть Бог»), либо потому, что оно остается справедливым независимо от своего содержания и даже независимо от истинного значения… … Философский словарь Спонвиля

Тавтология — ТАВТОЛОГИЯ повторение одних и тех же слов, выражений и т. п. как, например, в былине о Соловье разбойнике: Под Черниговым силушки черным черно, Черным черно, как черна ворона. Тавтология прием чрезвычайно употребительный в так наз … Словарь литературных терминов

тавтология — и, ж. tautologie f. 1. Повторное обозначение уже названного понятия словом или выражением, не уточняющим смысла выраженного понятия (используется как стилистический прием). БАС 1. Если одного общего места мало, то примемся за тавтологию этого… … Исторический словарь галлицизмов русского языка

Источник

Тавтология

Резюме

Использование в риторике

В преднамеренных рамках

Эжен Ионеско в своей пьесе « Носорог» показывает этот процесс, попирая законы логики с помощью туманных, но верных с грамматической и «механической» точки зрения тавтологий и силлогизмов ; Жан : «У меня есть сила, потому что у меня есть сила. «

Тавтологии в математической логике

В математической логике этот термин приобрел техническое значение, которое может отклоняться от здравого смысла.

При вычислении предикатов мы называем универсально допустимым утверждение (закрытая формула), которое истинно во всех моделях (где оно имеет значение). Это понятие в целом не разрешимо, истина не определяется механически, модели могут быть бесконечными.

Тавтологические объекты в математике

В математике мы используем прилагательное «тавтологический» для обозначения структур, которые естественным образом возникают из определения определенных объектов. Например :

Примеры тавтологических фигур

Тавтологии, которые стремятся подтвердить факт

Этот тип фразы обычно подразумевается в форме используемого предложения, часто для превращения его в слоган, особенно в рекламе, обеспечивая таким образом комический или привлекательный эффект:

Часто излишними считаются тавтологии, не обеспечивающие дополнительной точности.

Непроизвольные, даже неожиданные тавтологии

Это тавтологии, когда забывают или игнорируют значение или происхождение слов:

На самом деле этих тавтологий больше нет, этимология забыта.

Название места может выразить идею на забытом языке, тогда новые носители будут вводить повторение в новом названии. Но в большинстве случаев это перевод, а не тавтология.

Распространенные или пресловутые освященные выражения

Большинство этих лексикализованных выражений не являются тавтологиями.

Источник