Стягиваемая дуга что это
Хорды и дуги
Докажем ряд теорем, устанавливающих зависимость между хордами и их дугами в одной и той же окружности или в равных окружностях.
При этом будем иметь в виду дуги, меньшие полуокружности.
Теорема 1. Равные дуги стягиваются равными хордами.
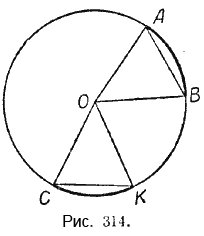
Пусть дуга АВ равна дуге СК. Требуется доказать, что и хорда АВ равна хорде СК (рис. 314).
Доказательство. Соединим концы хорд с центром окружности — точкой О. Полученные треугольники АОВ и КОС равны, так как имеют по две соответственно равные стороны (радиусы одной окружности) и по равному углу, заключённому между этими сторонами (эти углы равны, как центральные, соответствующие равным дугам). Следовательно, АВ = СК.
Теорема 2 (обратная). Равные хорды стягивают равные дуги.
Пусть хорда АВ равна хорде СК. Требуется доказать, что дуга АВ равна дуге СК (рис. 314).
Доказательство. Соединим концы хорд с центром окружности — точкой О. Полученные треугольники АОВ и КОС равны по трём соответственно равным сторонам. Следовательно, равны углы АОВ и СОК; но углы эти центральные, соответствующие дугам АВ и СК; из равенства этих углов следует равенство дуг: \(\breve <АВ>= \breve<СК>\).
Теорема 3. Большая дуга стягивается и большей хордой.
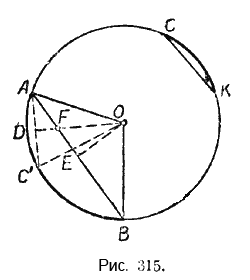
Пусть дуга АВ больше дуги СК (рис. 315).
Требуется доказать, что хорда АВ больше хорды СК.
Рассмотрим теперь треугольники ОАD и ОАЕ. В этих треугольниках гипотенуза ОА общая, а катет ОЕ меньше катета ОD, тогда по следствию из теоремы Пифагора катет АЕ больше катета АD. Но эти катеты составляют половины хорд АВ и АС’, значит, и хорда АВ больше хорды АС’. Вследствие равенства хорд АС’ и СК получаем
АВ > СК.
Теорема 4 (обратная). Большая хорда стягивает и большую дугу.
Пусть хорда А В больше хорды СК.
Требуется доказать, что дуга АВ больше дуги СК (рис. 315). Между дугами АВ и СК может существовать только одно из трёх следующих соотношений:
Но дуга AВ не может быть меньше дуги СК, так как тогда по прямой теореме хорда АВ была бы меньше хорды СК, а это противоречит условию теоремы.
Дуга АВ не может быть равна дуге СК, так как тогда хорда АВ равнялась бы хорде СК, а это тоже противоречит условию. Следовательно, \(\breve <АВ>> \breve<СК>\).
Свойство дуг, заключенных между параллельными хордами
Теорема. Дуги, заключённые между параллельными хордами, равны.
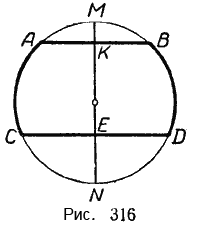
Пусть хорда AB параллельна хорде СD (рис. 316).
Требуется доказать, что \(\breve
Перегнём чертёж по диаметру MN так, чтобы правая часть совпала с левой.
Тогда точка В совпадёт с точкой А, так как они симметричны относительно оси MN (AB ⊥ MN по построению и AK = KB).
Аналогично, точка D совпадёт с точкой С. Отсюда \(\breve
Свойство дуг, заключённых между касательной и параллельной ей хордой
Теорема. Дуги, заключённые между касательной и параллельной ей хордой, равны.
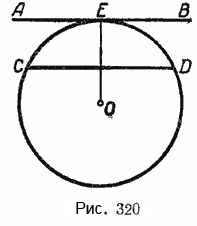
Пусть касательная АВ и хорда СD параллельны. Точка Е — точка касания прямой АВ с окружностью О (рис. 320).
Требуется доказать, что \(\breve
Для доказательства соединим точку касания Е с центром круга.
OE ⊥ AB, а так как СD || АВ, то OE ⊥ CD, а перпендикуляр к хорде, проведённый из центра той же окружности, делит стягиваемую ею дугу пополам.
Следовательно, \(\breve
Диаметр, перпендикулярный к хорде
Теорема 1. Диаметр, перпендикулярный к хорде, делит эту хорду и стягиваемые ею дуги пополам.
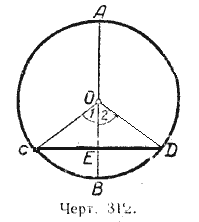
Пусть диаметр AB перпендикулярен к хорде CD (черт. 312). Требуется доказать, что
$$ CE = ED, \breve
Соединим точки С и D с центром окружности О. В равнобедренном треугольнике СОD отрезок ЕО является высотой, проведённой из вершины О на основание CD; следовательно, ОЕ является и медианой и биссектрисой, т. е. СЕ = ЕD и ∠1 = ∠2. Но ∠1 и ∠2 суть центральные углы. Отсюда равны и соответствующие им дуги, а именно
$$ \breve
Дуги CA и ВА также равны между собой, как дополняющие равные дуги до полуокружности.
Теорема 2 (обрaтная). Диаметр, проведённый через середину хорды, не проходящей через центр, перпендикулярен к ней и делит дуги, стягиваемые хордой, пополам.
Пусть диаметр AB делит хорду CD пополам. Требуется доказать, что AB ⊥ CD,
Соединим точки С и В с центром круга. Получим равнобедренный треугольник СОD, в котором ОК является медианой, а значит, и высотой. Следовательно, AB⊥CD, а отсюда (по теореме 1) следует, что
$$ \breve
Теорема 3 (обратная). Диаметр, проведённый через середину дуги, делит пополам хорду, стягивающую эту дугу, и перпендикулярен к этой хорде.
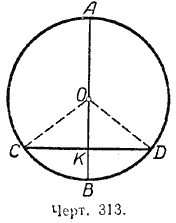
Пусть диаметр AB делит дугу СВD пополам (черт. 313). Требуется доказать, что
Соединим центр круга О с точками С и D. В равнобедренном треугольнике СОD отрезок ОК является биссектрисой угла СОD, так как по условию теоремы \(\breve
Окружность
Окружность — это геометрическая фигура, образованная замкнутой кривой линией, все точки которой одинаково удалены от одной и той же точки.
Точка, от которой одинаково удалены все точки окружности, называется центром окружности. Центр окружности обычно обозначают большой латинской буквой O:
Окружность делит плоскость на две области — внутреннюю и внешнюю. Геометрическая фигура, ограниченная окружностью, — это круг:
Построение окружности циркулем
Для построения окружности используют специальный прибор — циркуль:
Установим циркулю произвольный раствор (расстояние между ножками циркуля) и, поставив его ножку с остриём в какую-нибудь точку плоскости (например, на листе бумаги), станем вращать циркуль вокруг этой точки. Другая его ножка, снабжённая карандашом или грифелем, прикасающимся к плоскости, начертит на плоскости замкнутую линию — окружность:
Радиус, хорда и диаметр
Радиус — это отрезок, соединяющий любую точку окружности с центром. Радиусом также называется расстояние от точки окружности до её центра:
Все радиусы окружности имеют одну и ту же длину, то есть они равны между собой. Радиус обозначается буквой R или r.
Хорда — это отрезок, соединяющий две точки окружности. Хорда, проходящая через центр, называется диаметром окружности.
Диаметр обозначается буквой D. Диаметр окружности в два раза больше её радиуса:
Дуга — это часть окружности, ограниченная двумя точками. Любые две точки делят окружность на две дуги:
Чтобы различать дуги, на которые две точки разделяют окружность, на каждую из дуг ставят дополнительную точку:
Для обозначения дуг используется символ 
О хорде, которая соединяет концы дуги, говорят, что она стягивает дугу.
Хорда AB стягивает дуги 

Равные хорды
Выясним, какими свойствами обладают равные хорды и равные дуги.
Равные хорды равноудалены от центра окружности.


I. Рассмотрим треугольники AOB и COD.
2) OA=OB=OC=OD (как радиусы).
Следовательно, ∆AOB = ∆COD (по трём сторонам).
Из равенства треугольников следует равенство соответствующих углов: ∠A=∠C.
II. Рассмотрим прямоугольные треугольники AOF и COK.
2) ∠A=∠C (по доказанному).
Из равенства треугольников следует равенство соответствующих сторон: OF=OK.
Если хорды равноудалены от центра окружности, то они равны.
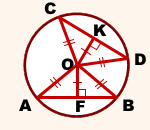
Соединим центр окружности с концами хорд.
I. Рассмотрим прямоугольные треугольники OKD и OFB.
Из равенства треугольников следует равенство соответствующих сторон:
II. Рассмотрим треугольники AOB и COD.
Так как OA=OB=OC=OD (как радиусы), треугольники AOB и COD — равнобедренные с основаниями AB и CD и высотами OK и OF соответственно.
По свойству равнобедренного треугольника, OK и OF — медианы, то есть AF=BF, CK=DK, откуда AB=CD.
Что и требовалось доказать.
Равные хорды стягивают равные дуги.
Дано : окр. (O;R), AB и CD — хорды, AB=CD,

Рассмотрим треугольники AOB и COD
2) OA=OB=OC=OD (как радиусы).
Следовательно, ∆AOB = ∆COD (по трём сторонам).
Из равенства треугольников следует равенство соответствующих углов: ∠AOB=∠COD.
Значит и дуги, на которые опираются эти центральные углы, также равны: ∪AB=∪CD
Хорды, стягивающие равны дуги, равны.
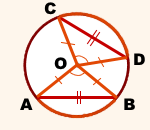
Соединим центр окружности с концами хорд.
Рассмотрим треугольники AOB и COD
Так как OA=OB=OC=OD (как радиусы), то треугольники AOB и COD — равнобедренные с основаниями AB и CD соответственно.
Так как ∪AB=∪CD (по условию), то ∠AOB=∠COD.
Из равенства треугольников следует равенство соответствующих сторон: AB=CD.
Центральные и вписанные углы
Центральный угол и вписанный угол
Окружность — замкнутая линия, все точки которой равноудалены от ее центра.
Определение центрального угла:
Центральный угол — это угол, вершина которого лежит в центре окружности.
Центральный угол равен градусной мере дуги, на которую он опирается.
На рисунке: центральный угол окружности EOF и дуга, на которую он опирается EF
Определение вписанного угла:
Вписанный угол — это угол, вершина которого лежит на окружности.
Вписанный угол равен половине центрального угла, опирающегося на ту же дугу, что и вписанный угол.
На рисунке: вписанный в окружность угол ABC и дуга, на которую он опирается AC
Свойства центральных и вписанных углов
Углы просты только на первый взгляд. Свойства центрального угла и свойства вписанного угла помогут решать задачки легко и быстро.
Угол AOC и угол ABC, вписанный в окружность, опираются на дугу AC, в этом случае центральный угол равен дуге AC, а угол ABC равен половине угла AOC.
ㄥADC = ㄥABC = ㄥAEC, поскольку все три угла, вписанные в окружность, опираются на одну дугу AC.
ㄥACB опирается на диаметр и на дугу AB, диаметр делит окружность на две равные части. Значит дуга AB = 180 ํ, ㄥCAB равен половине дуги, на которую он опирается, значит ㄥCAB = 90 ํ.
Если есть вписанный, обязательно найдется и описанный угол. Описанный угол — это угол, образованный двумя касательными к окружности. Вот так:
На рисунке: ㄥCAB, образованный двумя касательными к окружности. AO — биссектриса ㄥCAB, значит центр окружности лежит на биссектрисе описанного угла.
Для решения задачек мало знать, какой угол называется вписанным, а какой — описанным. Нужно знать, что такое хорда и ее свойство.
Хорда — отрезок, соединяющий две точки на окружности.
AB * AC = AE * AD
Получается, что стороны вписанного в окружность угла — это хорды.
ㄥBAC = ㄥCAB, поскольку лежат на хорде BC.
Примеры решения задач
Центральный, вписанные и описанные углы, как и любые другие, требуют тренировок в решении. Рассмотрите примеры решения задач и потренируйтесь самостоятельно.
Как решаем: окружность 360° − ⌒AC − ⌒CB = 360° − 200° − 80° = 80°
По теореме: вписанный угол равен дуге ½.
ㄥACB = ½ ⌒AB = 40°
Задачка 2. Дана окружность, ㄥAOC = 140°, найдите, чему равна величина вписанного угла.
Мы уже потренировались и знаем, как найти вписанный угол.
На рисунке в окружности центральный угол и дуга AC = 140°
Мы знаем, что вписанный угол равен половине центрального, то ㄥABC = ½ ⌒AC = 140/2 = 70°
Задачка 3. Чему равен вписанный в окружность угол, опирающийся на дугу, если эта дуга = ⅕ окружности?
⌒СB = ⅕ от 360° = 72°
Вписанный угол равен половине дуги, поэтому ㄥCAB = ½ от ⌒CB = 72° / 2 = 36°