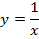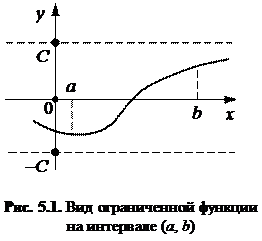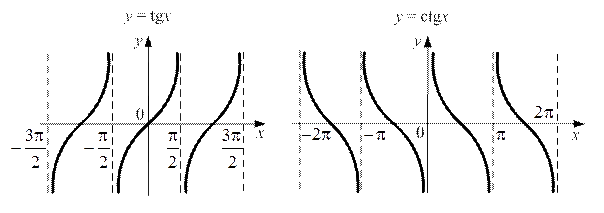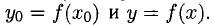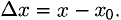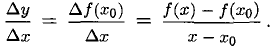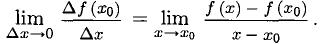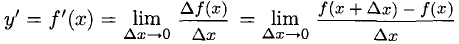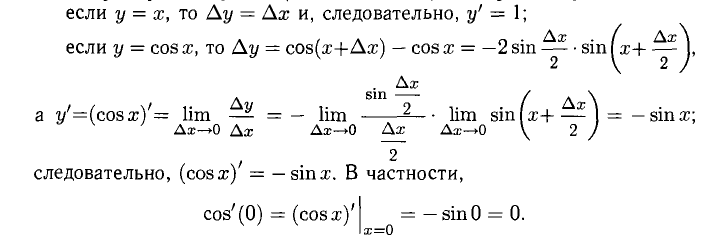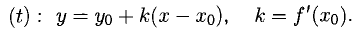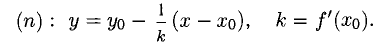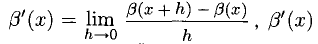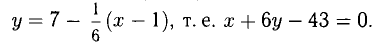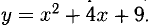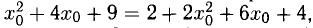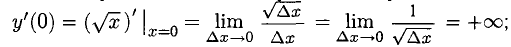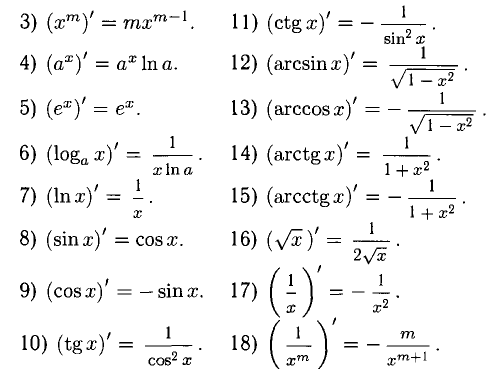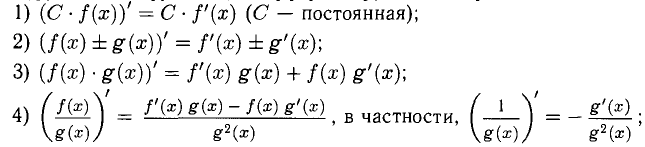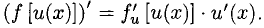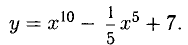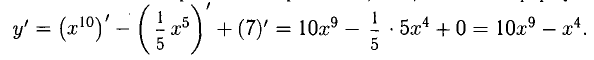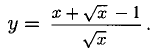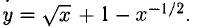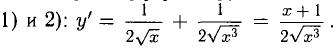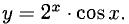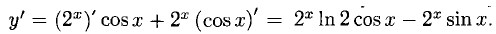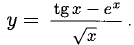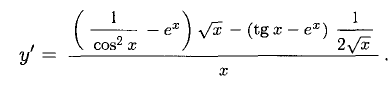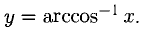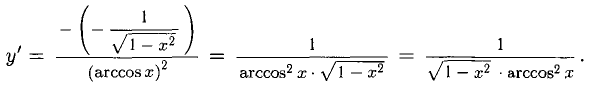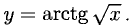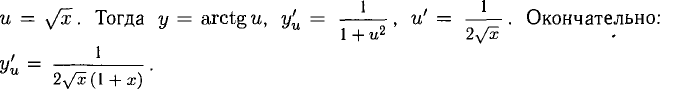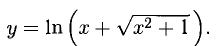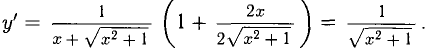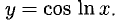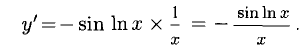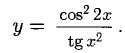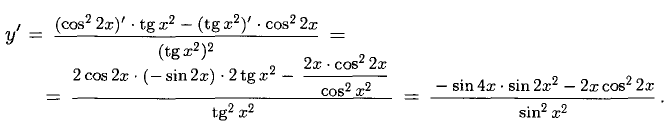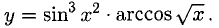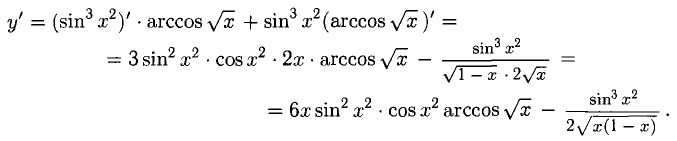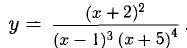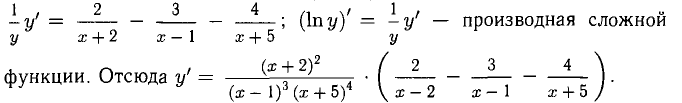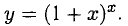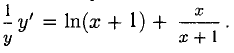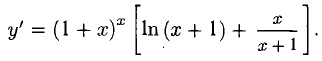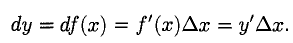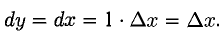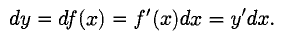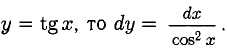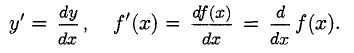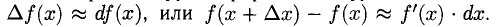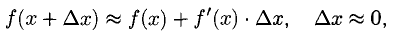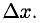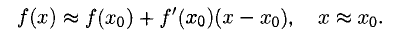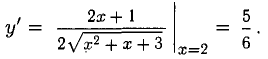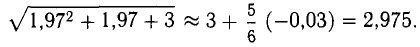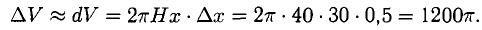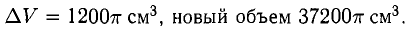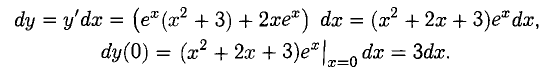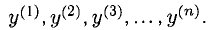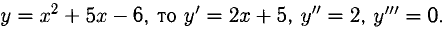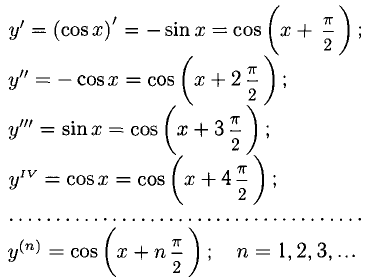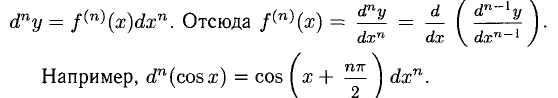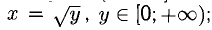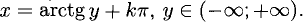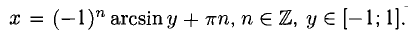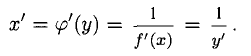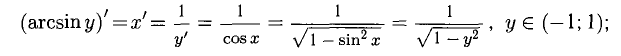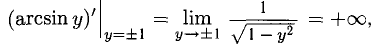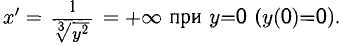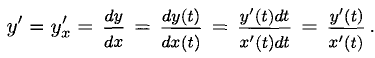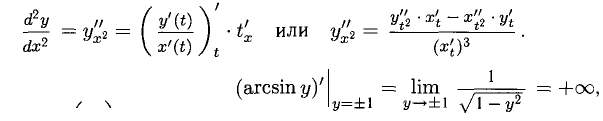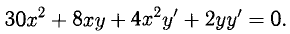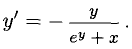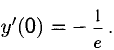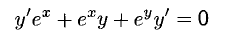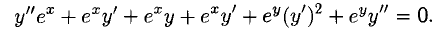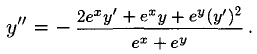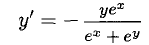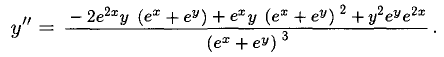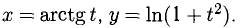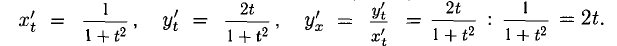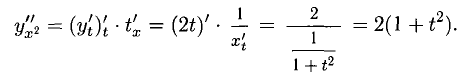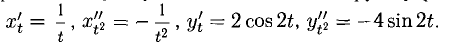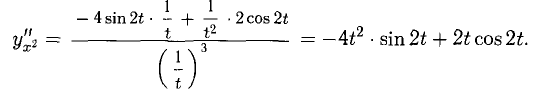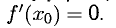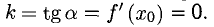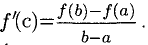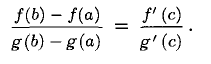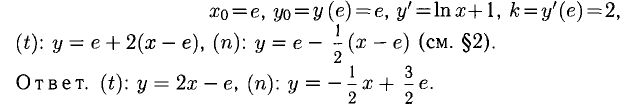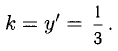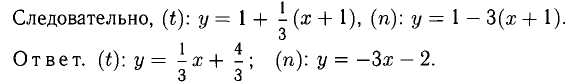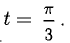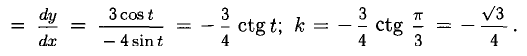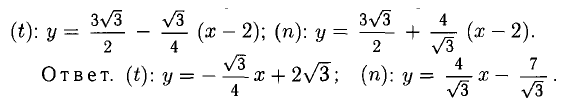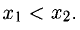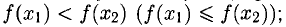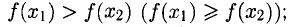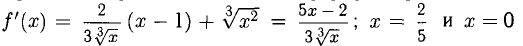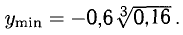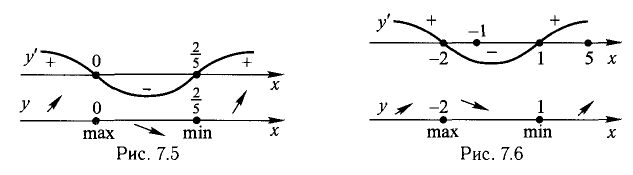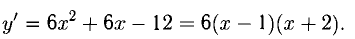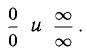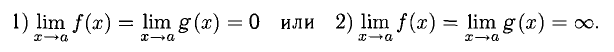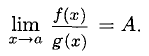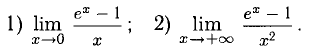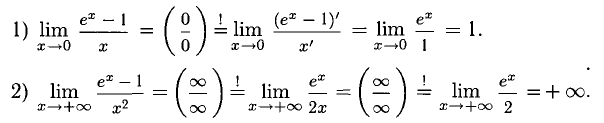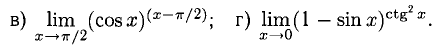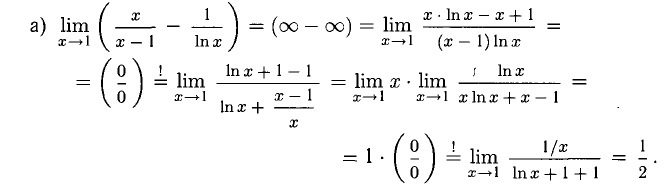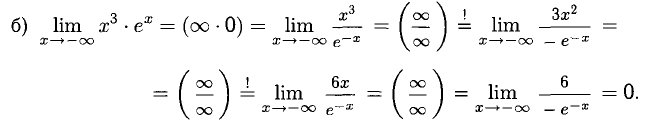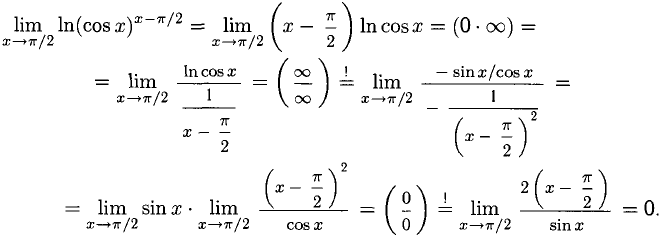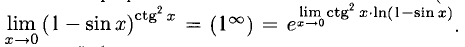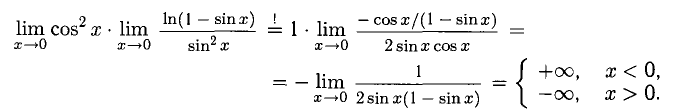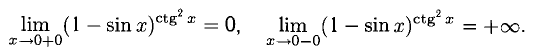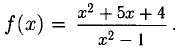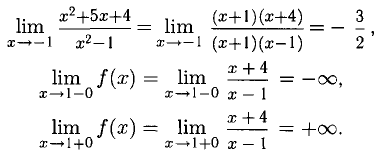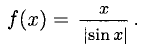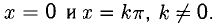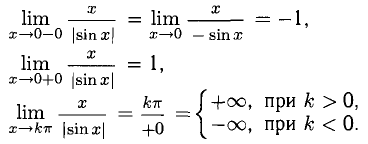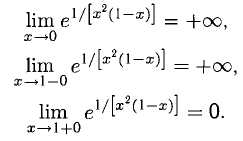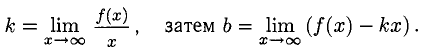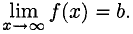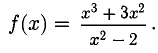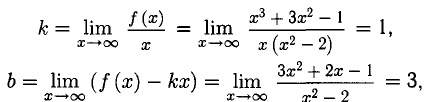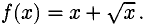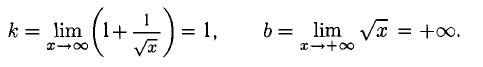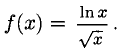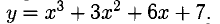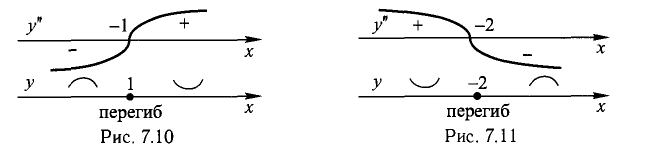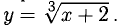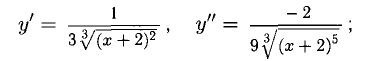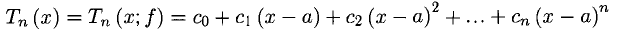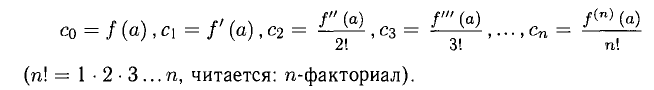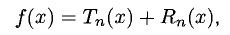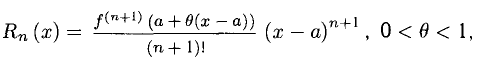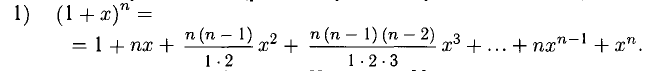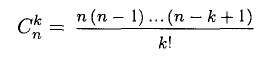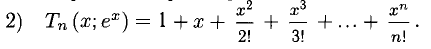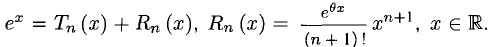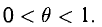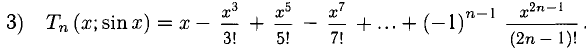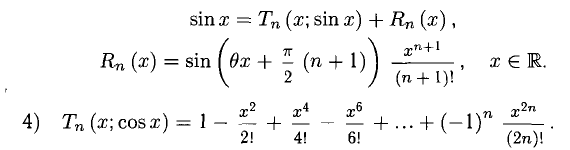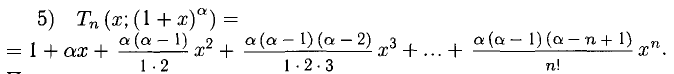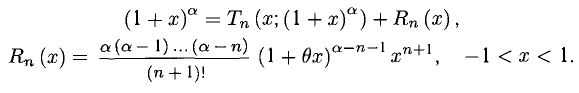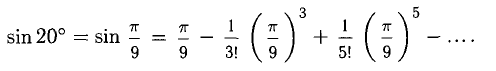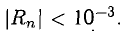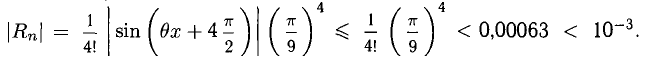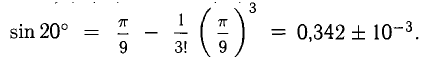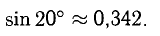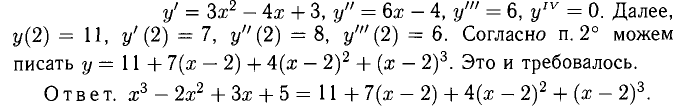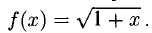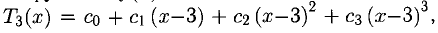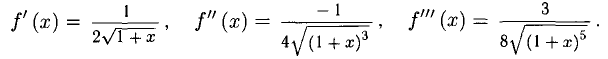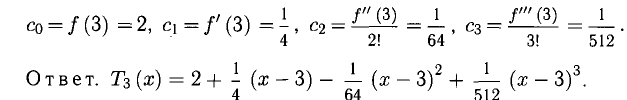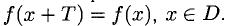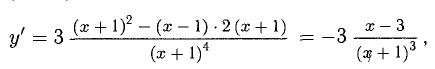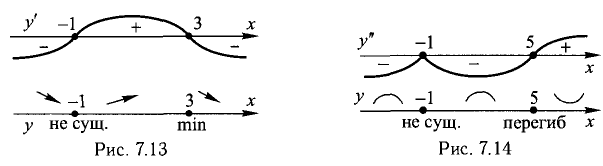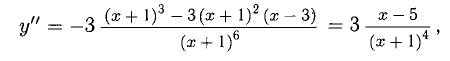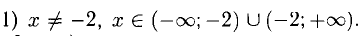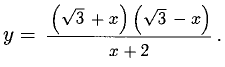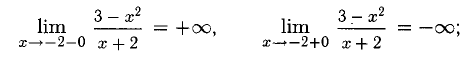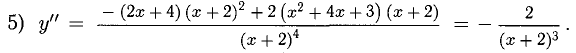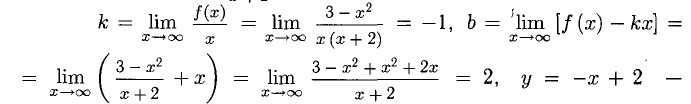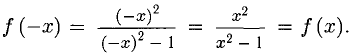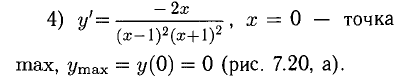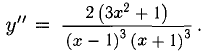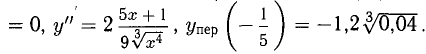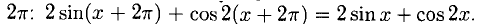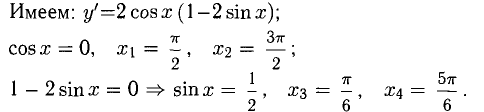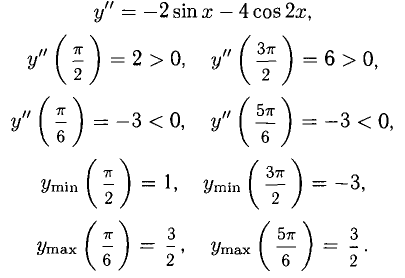Сформулируйте определение числовой функции одной переменной что такое график одной переменной
Тема 1. ФУНКЦИЯ ОДНОЙ ПЕРЕМЕННОЙ
1.1. Определение функции одной переменной
Определение. Пусть даны два множества X и Y. Если каждому элементу x из множества X по некоторому правилу f соответствует единственный элемент y из множества Y, то говорят, что на множестве X определена функция y = f ( x ) с областью определения X = D( f ) и областью изменения Y = E ( f ). При этом x считают независимой переменной, или аргументом функции, а y – зависимой переменной или функцией.
Частным значением функции y = f ( x ) при фиксированном значении аргумента x = x0 называют y 0 = f ( x 0 ).
1.2. Способы задания функции
1) Аналитический способ – способ задания функции с помощью формулы.
Различают несколько способов аналитического задания функции:
а) Функция задана явно формулой y = f ( x ).
б) Функция задана неявно уравнением, связывающем x и y : F( x ; y ) = 0.
Например: можно задать окружность 
3) Графический способ задания функции, когда зависимость функции от её аргумента задаётся графически.
1.3. Сложная и обратная функции
1.4. Элементарные функции
Основные элементарные функции:
Обратные тригонометрические функции :
Элементарной функцией называется функция, составленная из основных элементарных функций с помощью конечного числа операций сложения, вычитания, умножения, деления и суперпозиции.
Например: 
Графики обратных тригонометрических функций:
Что такое Функция?
7 класс, 11 класс, ЕГЭ/ОГЭ
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Понятие функции
Определение функции можно сформулировать по-разному. Рассмотрим несколько вариантов, чтобы усвоить наверняка.
1. Функция — это взаимосвязь между величинами, то есть зависимость одной переменной величины от другой.
Знакомое обозначение y = f (x) как раз и выражает идею такой зависимости одной величины от другой. Величина у зависит от величины х по определенному закону, или правилу, которое обозначается f.
Вывод: меняя х (независимую переменную, или аргумент) — меняем значение у.
2. Функция — это определенное действие над переменной.
Значит, можно взять величину х, как-то над ней поколдовать — и получить соответствующую величину у.
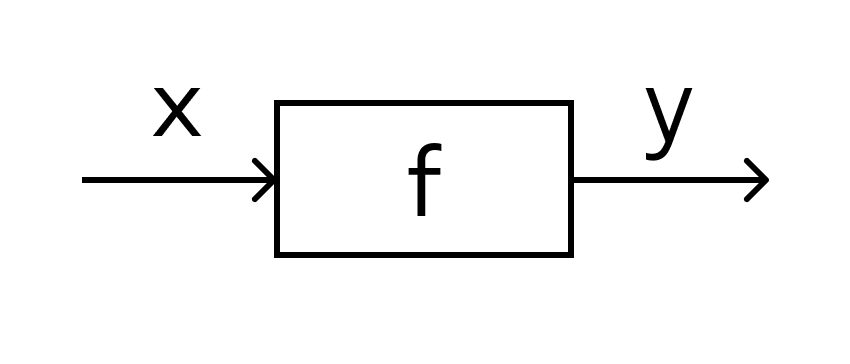
В технической литературе можно встретить такие определения функции для устройств, в которых на вход подается х — на выходе получается у. Схематично это выглядит так:
В этом значении слово «функция» используют и в далеких от математики областях. Например, так говорят о функциях ноутбука, костей в организме или даже о функциях менеджера в компании. В каждом перечисленном случае речь идет именно о неких действиях.
3. Функция — это соответствие между двумя множествами, причем каждому элементу первого множества соответствует один элемент второго множества. Это самое популярное определение в учебниках по математике.
Например, в функции у = 2х каждому действительному числу х ставит в соответствие число в два раза большее, чем х.
Область определения — множество х, то есть область допустимых значений выражения, которое записано в формуле.
Например, для функции вида
область определения выглядит так:
И записать это можно так: D (y): х ≠ 0.
Область значений — множество у, то есть это значения, которые может принимать функция.
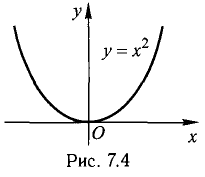
Например, естественная область значений функции y = x2 — это все числа больше либо равные нулю. Можно записать вот так: Е (у): у ≥ 0.
Для примера рассмотрим соответствие между двумя множествами — человек-владелец странички в инстаграм и сама страничка, у которой есть владелец. Такое соответствие можно назвать взаимно-однозначным — у человека есть страничка, и это можно проверить. И наоборот — по аккаунту в инстаграм можно проверить, кто им владеет.
В математике тоже есть такие взаимно-однозначные функции. Например, линейная функция у = 3х +2. Каждому значению х соответствует одно и только одно значение у. И наоборот — зная у, можно сразу найти х.
3.1. Определение функции одной переменной и её свойства
Повторим понятия функции и её свойства, которые нам потребуются для дальнейшего изложения материала.
Определение. Функция F(X) представляет собой правило, которое позволяет каждому значению хХ поставить в соответствие единственное значение Y = F(X)У, где х – независимая переменная (аргумент), Y – зависимая переменная (значение функции). Говорят, что функция F имеет Область определения D(F)=X и Область значений R(F)Y.
Существует три основных способа задания функции:
при Аналитическом способе задания функции зависимость между переменными определяется формулой;
при Табличном способе задания функции выписываются в определенном порядке значения аргумента и соответствующие значения функции;
при Графическом способе задания функции зависимость между переменными отражается с помощью графика.
Рассмотрим некоторые функциональные зависимости, используемые в экономике:
Функция спроса – зависимость спроса D на некоторый товар от его цены P;
Функция предложения – зависимость предложения S некоторого товара от его цены P;
Функция полезности – субъективная числовая оценка данным индивидом полезности И и количества Х товара для него;
Функция издержек – зависимость издержек I на производство Х единиц продукции;
Налоговая ставка – зависимость налоговой ставки N в процентах от величины годового дохода Q.
Все эти функции, кроме последней, весьма трудно выразить аналитически. При необходимости их находят путем кропотливого анализа. Последняя же функция, напротив, обычно довольно хорошо известна всему обществу и законодательно утверждена.
Определение. Функция F(X) имеет предел B, когда х стремится к а, если значения F(X) сколь угодно близко приближаются к числу B, когда значения переменной х сколь угодно близко приближаются к числу а.
Обозначение. 
Следует отметить, что в этом определении рассматриваются значения Х, сколь угодно близкие к числу А, но не совпадающие с А.
Определение. Если функция F(X) определена в точке а и выполняется равенство 
Определение. Функция, непрерывная в каждой точке своей области определения, называется Непрерывной функцией. В противном случае функцию называют Разрывной.
График непрерывной функции можно начертить без отрыва руки.
Непрерывные функции обладают следующими свойствами:
сумма или произведение непрерывных функций является непрерывной функцией;
отношение двух непрерывных функций является функцией непрерывной во всех точках, в которых знаменатель отношения не обращается в нуль.
Замечание. Метод, эффективный при анализе непрерывных функций, может оказаться неэффективным при исследовании разрывных функций, хотя обратное не исключается.
Если первая производная функции 
Если первая производная 
Первая производная 
Определение. Возрастающие, убывающие, неубывающие, невозрастающие функции называются Монотонными.
Замечание. Монотонная функция не обязательно должна быть непрерывной.
Решение. Находим производную: 


Исследуем критические точки, определяя знак 
Понятие функции одной переменной
Рассмотрим сначала понятие переменной величины, или просто переменной.
Переменная величина х определяется множеством тех значений, которые она может принять в рассматриваемом случае. Это множество X назовем областью изменения значений переменной x.
Главным предметом изучения в математике является, однако, не изменение одной переменной самой по себе, а зависимость между двумя или несколькими переменными при их совместном изменении. Во многих случаях переменные не могут принимать любую пару значений из своих областей изменения; если одной из них придано конкретное значение, то этим уже определяется и значение другой. Тогда первая из них называется независимой, а вторая – зависимой переменной.
Пусть даны две переменные x и y с областями изменения X и Y. Если при этом каждому элементу x 
Ясно, что при этом переменная x является независимой переменной. Ее часто называют аргументом функции.
Переменная y является зависимой переменной и называется значением функции, или просто функцией.
Множество X называется областью определения функции, а множество Y — областью ее значений.
Существует ряд способовзадания функции:
а) наиболее простой — аналитический способ, т. е. задание функции в виде формулы. Если область определения функции X при этом не указана, то под X подразумевается множество значений x, при которых формула имеет смысл;
б) графическийспособ. Этот способ особенно нагляден. Для функции одной переменной y = f(x) используется координатная плоскость (xy).
Совокупность точек y, соответствующих заданным значениям x, определяет график функции на плоскости (xy);
в) табличный способ. Он часто используется, когда независимая переменная x принимает лишь конечное число значений.
5.2. Основные свойства функций
Рассмотрим основные свойства функций, которые упрощают проведение их исследования:
Четность. Функция y = f(x) называется четной, если для любого значения x, принадлежащего области определения функции X, значение (–x) тоже принадлежит X и при этом выполняется
График четной функции симметричен относительно оси ординат.
Функция y = f(x) называется нечетной, если для любого x 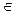
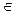
График нечетной функции симметричен относительно начала координат.
Если функция y = f(x) не является ни четной, ни нечетной, то ее часто называют функцией общего вида.
Монотонность. Функция y = f(x) называется возрастающейна некотором интервале (a, b), если для любых x1, x2 
Возрастающую и убывающую на интервале (a,b) функции называют монотонными на этом интервале, а сам интервал (a,b) — интервалом монотонности этих функций.
В некоторых учебниках такие функции называют строго монотонными, а монотонными называют неубывающую и невозрастающую на рассматриваемом интервале функции (вместо строгих неравенств для функций пишутся нестрогие).
Ограниченность. Функция y = f(x) называется ограниченной на интервале (a, b), если существует такое число С > 0, что для любого x 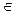
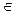
Аналогичное определение ограниченности можно дать для любого вида промежутка.
Периодичность.Функция y = f(x) называется периодической, если существует такое число t, что для любого x 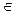
Наименьшее из таких чисел t называется периодом функции и обозначается Т.
Характерным признаком периодичности функций является наличие в их составе тригонометрических функций.

К элементарным функциям относятся:
а) простейшие элементарные функции
1. Константаy = c, где с — постоянное для данной функции действительное число, одно и то же для всех значений x.
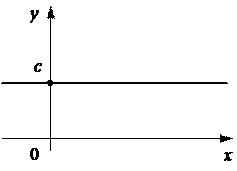 |
2. Степенная функция 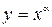
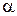
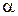
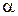
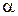
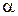
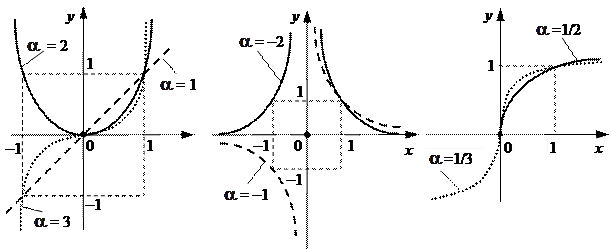 | |
|
3. Показательная функция y = a x (a > 0; a 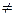
 |
4. Логарифмическая функция y = loga x (a > 0; a 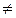
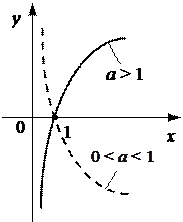 |
5. Тригонометрические функции: y = sin x, y = cos x, y = tg x, y = ctg x.
6. Обратные тригонометрические функции.
y = arcsin x y = arccos x
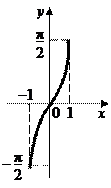 |  |
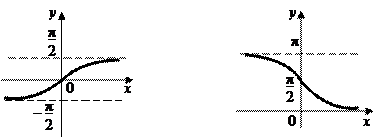 |
Кроме перечисленных простейших элементарных функций аргумента x к элементарным функциям также относятся функции, аргументами которых являются тоже элементарные функции, а также функции, полученные путем выполнения конечного числа арифметических действий над элементарными функциями. Например, функция
тоже является элементарной функцией.
Функции, аргументами которых являются не независимые переменные, а другие функции, называются сложными функциями или суперпозициями функций. Пусть даны две функции: y = sinx и z = log2 y. Тогда сложная функция (суперпозиция функций) может иметь вид
Также можно ввести понятиеобратной функции.Пусть y = f(x) задана в области определения X, а Y — множество ее значений. Выберем какое-нибудь значение y = y0 и по нему найдем x0 так, чтобы y0 было равно f(x0).Подобных значений x0 может оказаться и несколько.
Таким образом, каждому значению y из Y ставится в соответствие одно или несколько значений x. Если такое значение x только одно, то в области Y может быть определена функция x = g(y), которая называется обратной для функции y = f(x).
Следовательно, функция x = loga y является обратной для функции y = a x на множествах X и Y. Так как принято у любой функции независимую переменную обозначать x, то в этом случае говорят, что y = f(x) и y = g(x) — обратные функции.

Дифференциальное исчисление функции одной переменной с примерами решения и образцами выполнения
Страница содержит справочный материал по курсу «Дифференциальное исчисление функций одной переменной», подробно разобраны методы решения типовых задач.
Определение производной
1°. Производная непрерывной функции 
1) Вычислить
2) Составить приращение функции 
3) Составить отношение приращений
4) Найти предел
Если предел существует и конечен, то он обозначается 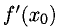
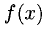
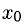
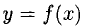
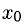
2°. Если вместо фиксированной точки хо взять переменную величину х, то производная
будет функцией от х.
Число 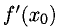
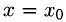
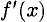
Например, если у = С (С — константа), то
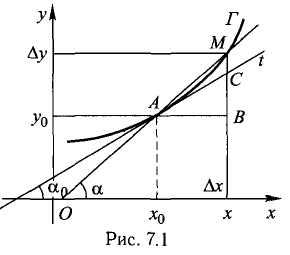
Геометрическая, механическая и экономическая интерпретации производной
1°. Выясним геометрический смысл отдельных пунктов определения производной, исходя из рис. 7.1, где изображен график Г возрастающей функции, а 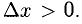
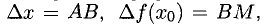
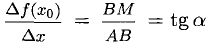
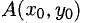
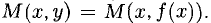
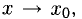
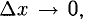
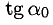
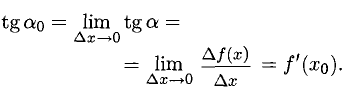
Вывод. Существование производной 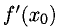
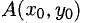
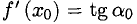
2°. Прямая, перпендикулярная касательной в точке касания 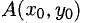
3°. Если S = S(t) — путь, пройденный материальной точкой М за время t, то 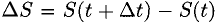
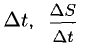
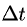
— мгновенная скорость точки М в момент времени t.
4°. Пусть 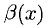
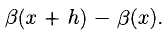
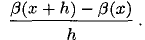
— коэффициент изменения прибыли, показывающий динамику ее изменения; 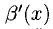
Примеры с решениями
Пример:
Составить уравнения касательной и нормали к параболе в 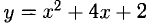
Решение:
Точка А( 1,7) лежит на параболе. Находим 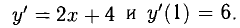
Пример:
Составить уравнение прямой, проходящей через точку В(-1,2) касательно параболе
Решение:
Точка В(-1,2) не лежит на параболе, поэтому способ, приведенный выше, неприменим. Обозначим через 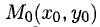
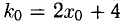
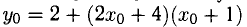
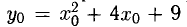
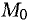
т.е 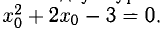
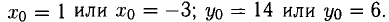
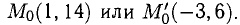
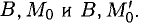
Связь дифференцируемости с непрерывностью
1°. Напомним: функция, имеющая конечную производную в данной точке, называется дифференцируемой в этой точке, в противном случае — недифференцируемой.
Теорема:
Если функция дифференцируема в данной точке, то в этой точке она непрерывна.
Из существования 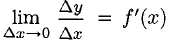
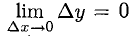
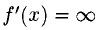
2°. Функция, непрерывная в данной точке, не обязательно дифференцируема в этой точке.
функция 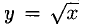
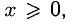
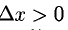
функция 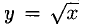
3°. Функция, дифференцируемая в каждой точке данного интервала, называется дифференцируемой в этом интервале. Функция с непрерывно изменяющейся производной (касательной) называется гладкой. График функции у = |x| не гладкий при х=0 (имеет угол).
Таблица производных и правила дифференцирования
1°. Дифференцирование основных элементарных функций осуществляется при помощи следующих формул:

Формулы 16)-18) являются частными случаями 3). Все формулы необходимо знать наизусть.
2°. Функции, составленные из основных при помощи арифметических действий (сложения, вычитания, умножения, деления) и композиции (функция от функции), дифференцируются по правилам:
5) если f(u) и и = u(x) — дифференцируемые функции, то производная сложной функции
Примеры с решениями
(во всех примерах найти у’)
Пример:
Решение:
Применяем правила 1) и 2), а также формулы 3) и 1):
Пример:
Сначала преобразуем:
Теперь дифференцируем, используя формулы 1), 16), 3) и правила
Пример:
Решение:
Имеем производную произведения (правило 3)) функций, содержащихся в формулах 4) и 9):
Пример:
Решение:
Применяем правило 4), формулы 10), 5), 16). Производная частного:
Пример:
Решение:
Применяем правило 4), частный случай, и формулу 13).
Пример:
Решение:
Применяем правило 5), формулы 14) и 16). Положим
Пример:
Решение:
Положим 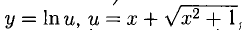
Пример:
у = cos Inx.
Решение:
Обозначим 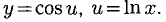
Пример:
Решение:
Дифференцируем частное двух сложных функций:
Пример:
Решение:
Имеем дело с производной произведения сложных функций:
Примечание:
При дифференцировании функций, состоящих из большого количества множителей, или функций вида 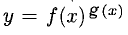
Пример:
Решение:
Находим сначала ln у, затем продифференцируем обе части полученного равенства, причем левую часть lп y(х) — как сложную функцию:
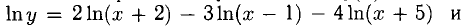
Пример:
Решение:
Берем логарифм обеих частей равенства 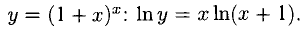
Дифференциал функции и ее линеаризация
1°. Дифференциалом дифференцируемой функции 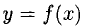
Для функции у = х ее дифференциал равен
Дифференциал аргумента совпадает с его произвольным приращением, поэтому дифференциал функции записывают в виде
Например, если
Из определения дифференциала функции можно записать новое, формальное определение производной:
Это обозначение принято в дифференциальных уравнениях.
2°. Из рис. 7.1 видно, что 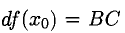
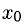
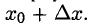
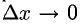
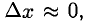
Отсюда получаем приближенное равенство
которое называется линеаризацией функции f(x) в точке х. Геометрически это означает замену дуги Г графика функции f(x) отрезком касательной t, что возможно при достаточно малых
3°. Линеаризацию функции в фиксированной точке 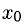
Примеры с решениями
Пример:
Вычислить приближенно значение функции 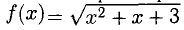
Решение:
Принимаем 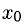
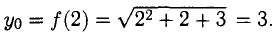
Так как 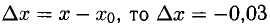
Пример:
Вычислить приближенно увеличение объема цилиндра с высотой H = 40 см и радиусом основания R = 30 см при увеличении радиуса на 0,5 см.
Решение:
Объем цилиндра V при постоянной высоте H и переменном радиусе х есть функция от х: 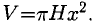
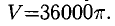
Пример:
Найти дифференциал функции 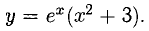
Решение:
Производные и дифференциалы высших порядков
1°. Предположим, что производная 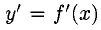
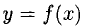
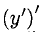
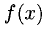
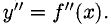
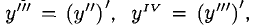
Если у = cosx, то производную любого порядка этой функции найдем следующим образом:
2°. Дифференциалы высших порядков определяются так:
Дифференцирование обратных функций. Дифференцирование функций, заданных неявно и параметрически
1°. Пусть у = f (х) — функция, определенная и непрерывная на отрезке [а; b] и f (а) = A, f(b) = В. Если различным значениям 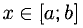
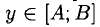
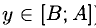
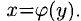
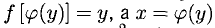
Например, функция 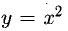
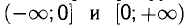
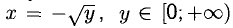
у = tgx обратима в интервале 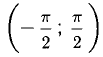
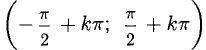
2°. Если различным значениям 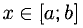
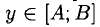
Например, непрерывная функция 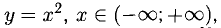
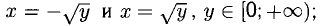
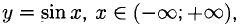
3°. Если у = f(x) дифференцируема на отрезке [а; b] и 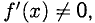
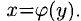
Например, пусть 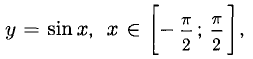
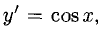
обратной функции 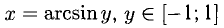
это согласуется с тем, что
если 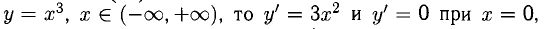
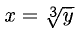
5°. Если функция у = у(х) задается параметрически, т.е. при помощи двух функций 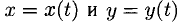
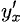
Вторую производную 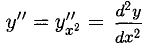
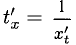
Примеры с решениями
Пример:
Решение:
Считаем, что у = у(х). Продифференцируем левую часть данного уравнения как сложную функцию, приравняем нулю полученное выражение и найдем у’:
Пример:
Найти у’, если 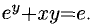
Решение:
Дифференцируем обе части данного равенства, имея в виду, что 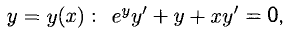
В частности, если х = 0, то у =1 и
Пример:
Для функции у(х), определенной неявно уравнением 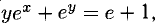
Решение:
После двух последовательных дифференцирований данного уравнения с учетом у = у (х) получаем
Из второго равенства находим
Из первого равенства находим
и подставляем это в предыдущее равенство. После упрощения получаем
Пример:
Найти у’ и у», если
Решение:
При помощи первой из формул для 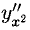
Пример:
Решение:
Для определения у» будем использовать вторую формулу. Сначала находим:
Основные теоремы дифференциального исчисления
1°. Точка 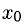
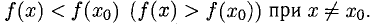
Теорема Ферма:
Если дифференцируемая функция f(x) имеет экстремум в точке 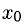
В точке экстремума касательная горизонтальна, а для нее
Теорема Ролля:
Предположим, что функция f(x) непрерывна на отрезке [а,b], дифференцируема в интервале (а,b) и f(a) = f (b). Тогда существует хотя бы одна точка 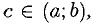
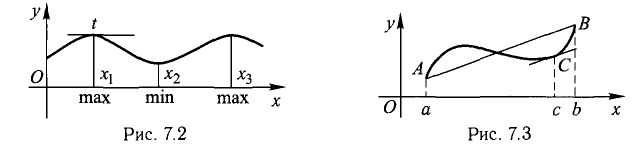
Теорема Лагранжа:
Предположим, что функция f(x) непрерывна на отрезке [а; b] и дифференцируема в интервале (а; b). Тогда существует хотя бы одна точка с € (а; b), такая, что f(b)-f(a)=f'(c)(b-a), или
Геометрически теорема 4 означает что на кривой существует хотя бы одна точка, в которой касательная параллельна хорде АВ, f ‘(с) — ее угловой коэффициент (рис. 7.3).
Теорема Коши:
Пусть f(x) и g(x) — две функции, непрерывные на отрезке [а; b] и дифференцируемые в интервале (а; b), причем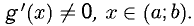
Примеры с решениями
Пример:
Проверить, справедлива ли теорема Ролля для функции 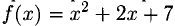
Решение:
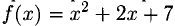
Пример:
Найти точку с, о которой идет речь в теореме Лагранжа, для функции 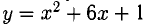
Решение:
Нам надо решить уравнение у’ = 2x + 6 = 8. Находим х = 1, т. е. с имеет координаты (1,8). Касательная в этой точке параллельна хорде АВ.
Пример:
Решение:
Пример:
Составить уравнения касательной и нормали к кривой 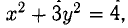
Решение:
При у = 1 находим х = —1 и х = 1. В задаче идет речь о точке A(-1,1). Находим у’ из уравнения 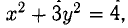
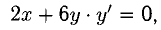
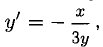
Пример:
Составить уравнения касательной и нормали к эллипсу 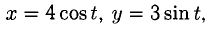
Решение:
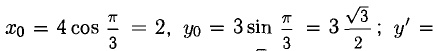
Исследование на монотонность и экстремум
1°. Предположим, что функция f(x) непрерывна в интервале (а; b) и 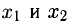
Функция f(x) называется в этом интервале:
— возрастающей (неубывающей), если
— убывающей (невозрастающей), если
— монотонной, если она либо возрастающая (неубывающая), либо убывающая (невозрастающая).
Например, функция 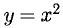
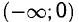
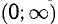
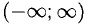
Теорема:
Если f ‘(х) > 0 при 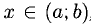
— критические точки f (х). На верхней оси диаграммы (рис. 7.5) обозначено распределение знаков f ‘(х), а на нижней — поведение функции f (х) согласно теоремам 6 и 7.
Ответ. В интервалах 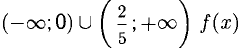
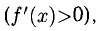
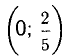
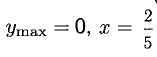
Исследовать на монотонность и экстремумы функцию 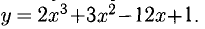
Решение:
Находим у’ и исследуем ее знак:
Раскрытие неопределенностей
1°. Неопределенности видов
Пусть функции f(x) и g(x) непрерывны и дифференцируемы в некоторой окрестности точки х = а, кроме, быть может, самой точки а (при этом а может быть конечным числом или 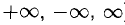
Правило Лопиталя. Если существует предел 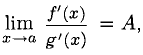
Правило Лопиталя позволяет при помощи производных раскрыть неопределенность: в случае 1) вида 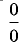
При необходимости правило Лопиталя можно применить повторно или несколько раз при соответствующих условиях на 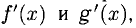
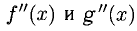
Например, вычислим пределы:
В первом случае имеем неопределенность вида 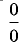
вида 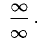
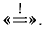
2°. При помощи правила Лопиталя можно раскрыть неопределенности других видов: 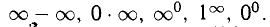
В нижеследующих примерах необходимые преобразования выполним по ходу решения. Заметим, что иногда приходится избавляться от «мешающих» множителей — это делается при помощи теоремы о пределе произведения.
Примеры с решениями
Пример:
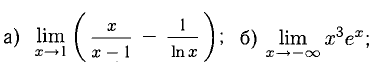
Визуальный обзор указывает на наличие разных неопределенностей.
Решение:
Здесь мы избавились от множителя х, усложняющего производную, и дважды применили правило Лопиталя.
Рекомендуем вычислить этот предел при помощи замены х = —t
в) Найдем предел логарифма выражения, стоящего под знаком предела. Воспользуемся теоремой о возможности перехода к пределу под знаком непрерывной функции:
Вывод: искомый предел равен е° = 1.
г) Этот пример, как и предыдущий, можно решить при помощи основного показательно-логарифмического тождества: 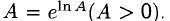
Для компактности выражений берем отдельно предел показателя:
Получили два различных односторонних предела, следовательно, искомый предел не существует. Тем не менее зафиксируем односторонние пределы:
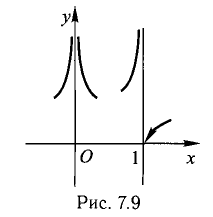
Асимптоты
Вертикальные асимптоты
Напомним, что если х = а — точка разрыва функции f(x) и 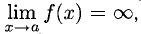
Примеры с решениями
Требуется определить точки разрыва данной функции, исследовать их характер, найти вертикальные асимптоты и построить график в окрестности точки разрыва.
Пример:
Решение:
Пример:
Решение:
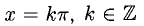
Ответ, x = 0 — точка разрыва первого рода со скачком 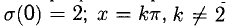
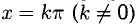
Пример:
Решение:
x = 0 и x = 1 — точки разрыва,
Ответ, х = 0, х =01 — точки разрыва второго рода, прямые х = 0, х = 1 — вертикальные асимптоты (рис. 7.9).
Наклонные асимптоты. Горизонтальные асимптоты
Прямая с уравнением у = kx + b называется наклонной асимптотой графика функции f(x), если 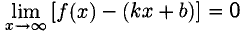
После деления на х выражения, стоящего под знаком предела, и перехода к пределу получаем
Горизонтальная асимптота является частным случаем наклонной при 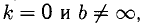
Примеры с решениями
Требуется найти наклонные асимптоты графика данной функции, если они есть.
Пример:
Решение:
y = х + 3 — наклонная асимптота.
Пример:
Решение:
Функция определена только при 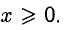
Пример:
Решение:
Данная функция определена при x > 0, поэтому 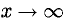
у = 0 — горизонтальная асимптота (вправо, 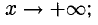
Исследование функций на выпуклость, вогнутость и перегиб при помощи второй производной
1°. Дифференцируемая функция f (х) называется выпуклой (вогнутой) в некотором интервале, если ее график расположен ниже (выше) касательной, проведенной в каждой его точке с абсциссой в этом интервале.
Теорема:
Если f»(x) 0, 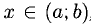
2°. Точка 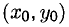
Теорема:
Если f»(x) 0 при 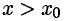
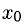
Следует из теоремы 9.
Примеры с решениями
Пример:
Исследовать на выпуклость, вогнутость и перегиб функцию
Решение:
Имеем: 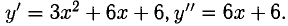
Пример:
Исследовать на выпуклость, вогнутость и перегиб функцию
Решение:
Надлежит исследовать знак второй производной.
Применение высших производных
1°. Запись 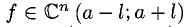
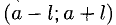
2°. Многочлен степени не выше п
называется многочленом Тейлора функции f(x) с центром в точке х = а, если его коэффициенты 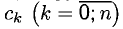
Теорема Тейлоро:
Если 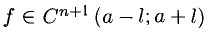
— остаточный член формулы Тейлора в форме Лагранжа. Величина Rn(x) — бесконечно малая порядка (п+1) относительно (х — а) в окрестности точки а.
При а = 0 многочлен Тейлора называется также многочленом Маклорена. Многочлен Тейлора-Маклорена служит достаточно хорошим средством приближенного представления функции и широко применяется в приближенных вычислениях.
3°. Многочлены Маклорена для некоторых из элементарных функций имеют следующий вид (рекомендуется получить их и знать).
Эта формула называется биномом Ньютона. Множители
— биномиальные коэффициенты — находят широкое применение в комбинаторике и теории вероятностей.
Здесь и далее
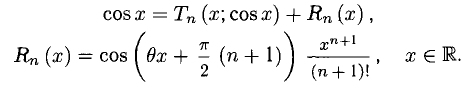
Примеры с решениями
Пример:
Вычислить с точностью до 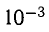
Решение:
Число членов в правой части следует брать из условия
Ответ.
Пример:
Многочлен 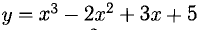
Решение:
Пример:
Написать многочлен Тейлора третьей степени с центром в точке х = 3 для функции
Решение:
где 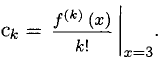
Вычислим теперь 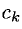
Исследование функций и построение графиков
Построению графика данной функции у = f (х) предшествует полное ее исследование, включающее выявление характерных свойств и особенностей этой функции. К ним относятся: область определения D = D ( f ), область изменения E(f), непрерывность, дифференцируемость, четность, нечетность, ограниченность, периодичность функции, ее интервалы знакопостоянства, монотонности, выпуклости/вогнутости, наличие асимптот (вертикальных, горизонтальных, наклонных). Кроме этого, необходимо определить характерные точки: разрыва, пересечения графика с координатными осями, точки экстремума (максимума, минимума), точки перегиба и проч.
Приведем сначала определения тех понятий, которые не встречались выше.
Напомним, что функция у = f (х) называется:
— периодической, если существует число Т > 0, такое, что
Исследование функции выполняется по определенной схеме, пункты которой установим по ходу исследования. Заметим, что если по некоторым признакам мы не имеем позитивной информации, то соответствующий пункт может быть опущен.
Примеры построения графиков
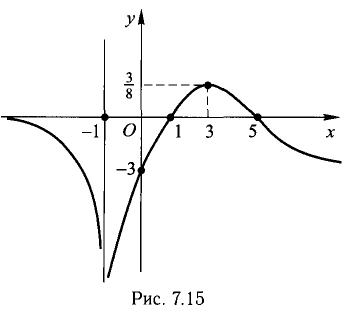
Пример:
Исследовать функцию 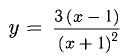
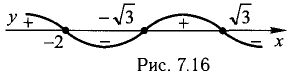
1) Находим область определения:
2) Простейшие свойства — четность, нечетность, периодичность, ограниченность. Таких свойств не обнаруживаем.
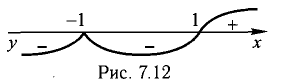
3) Определим точки пересечения графика с координатными осями и интервалы знакопостоянства функции.
5) Исследуем функцию на монотонность и экстремум (рис. 7.13):
х = 3 — точка max, 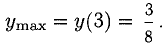
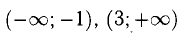
Везде «не сущ.» означает «не существует».
6) Исследуем на выпуклость, вогнутость и перегиб (рис. 7.14)
х = 5 — абсцисса точки перегиба, 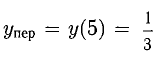
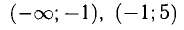
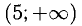
7) Исследуем поведение функции на бесконечности и определим горизонтальные и (или) наклонные асимптоты. Имеем: 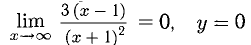
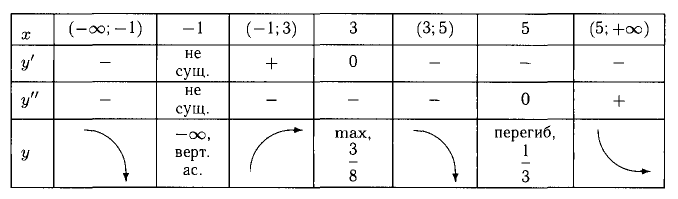
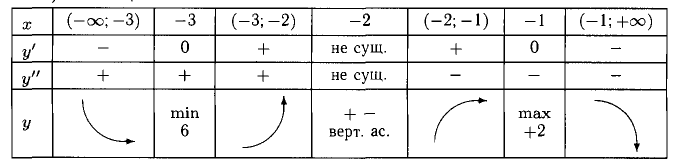
8) Результаты исследования поместим в таблицу для компактности:
В первую строку таблицы заносим точки разрыва, экстремума, перегиба и интервалы между ними. Во второй строке располагается
информация о f'(x) и ее знаках, в третьей строке о f»(x) и ее знаках. Третья строка показывает вид графика в соответствующих интервалах и характерные его точки.
9) Построение графика начинается с построения асимптот и точек с известными координатами (рис. 7.15). Приближение графика к асимптоте должно быть плавным и создавать впечатление неограниченного продолжения.
Пример:
Исследовать функцию 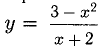
2) График пересекает ось Ох, если 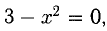
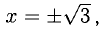
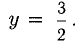
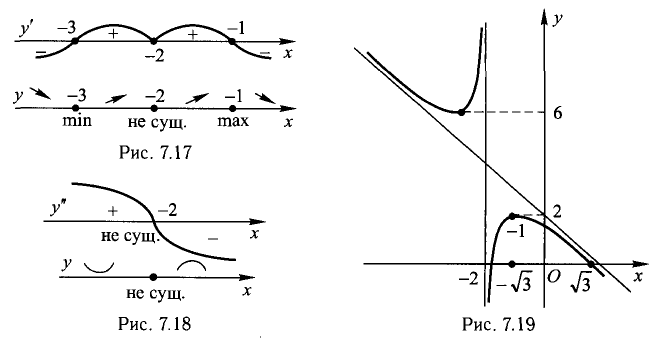
х =-2 — вертикальная асимптота вверх и вниз.
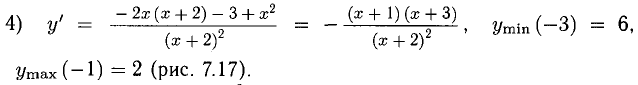
Точек перегиба нет, схема выпуклости/вогнутости представлена на рис. 7.18.
6) Имеем 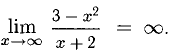
уравнение наклонной асимптоты в обе стороны.
8. График построен (рис. 7.19).
Примечание. Последовательность действий может быть изменена (вертикальные асимптоты можно искать параллельно с горизонтальными и наклонными), а некоторые пункты схемы могут быть опущены, если это не влияет на выводы исследования.
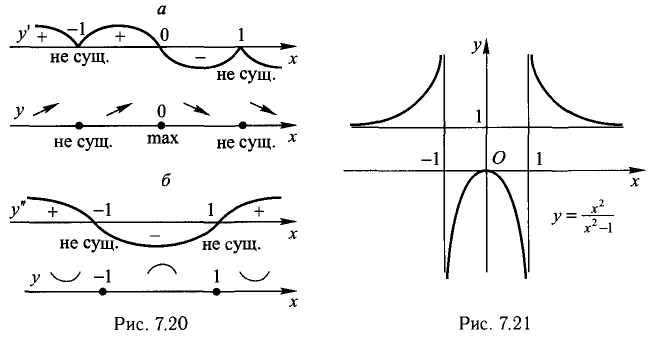
Пример:
Исследовать функцию 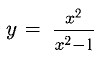
Укажем основные элементы исследования и приведем график.
1) 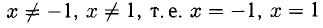
2) Функция четная, так как
График функции симметричен относительно оси Оу.
3) 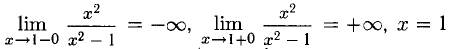
асимптота вниз и вверх (х =-1 — вертикальная асимптота вверх и вниз, по четности).
5)
Точек перегиба нет, схема выпуклости/вогнутости представлена на рис. 7.20, б.
6) 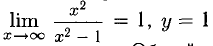
Пример:
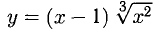
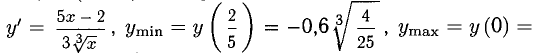
Никаких асимптот нет.
Пример:
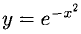
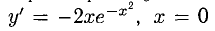
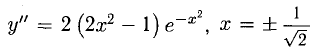
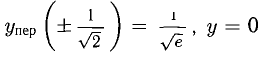
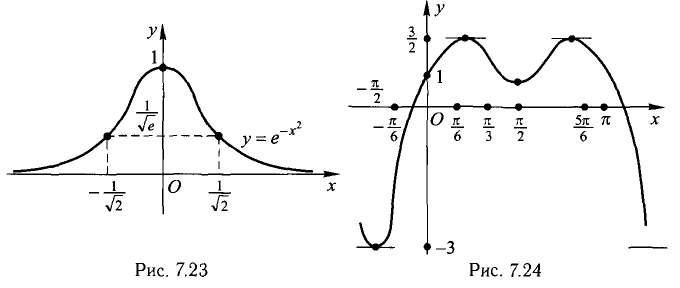
Пример:
у = 2 sin x + cos2x (рис. 7.24).
Функция определена при 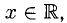
Исследование на экстремум проводим по такому признаку. Если 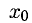
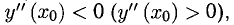
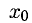
Функция имеет 4 стационарных точки: 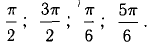
Функция не имеет асимптот.
Решение заданий и задач по предметам:
Дополнительные лекции по высшей математике:
Образовательный сайт для студентов и школьников
Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.
© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института