рандомить что это такое
Что значит «рандомно» в интернет-сленге?
Современный интернет-сленг ежедневно пополняется новыми словами и выражениями. Они заимствуются из других языков и профессиональных жаргонизмов, подстраиваются под нужды пользователей сети и прочно закрепляются в их речи. Одним из таких терминов является слово «рандомно». Что оно обозначает? Откуда появилось и как используется сейчас?
Значение и происхождение
Термин «рандомно» произошел от английского random (случайный, произвольный, хаотичный). Внедрился в русское интернет-сообщество благодаря геймерскому комьюнити.
Еще в «древних» пиксельных RPG присутствовал элемент случайности в выпадении лута после поединков. В современных РПГ и ММОРПГ этот принцип сохраняется.


В некоторых играх можно выбрать рандомный мир для выживания или персонажа для сражения со случайным набором характеристик. Это позволяет игроку прокачивать свои умения в любых условиях.
Также считается, что слово «рандомно» пришло из языка программирования, а точнее, произошло от функции random (случайная последовательность чисел).
Современное использования термина
Выражение давно используется за пределами гейм-комьюнити и среды программирования. Сейчас его употребляют повсеместно. Например, термин «рандомно» применяется во время розыгрыша каких-либо предметов в соцсетях (от стикеров Вконтакте до автомобилей). Так, во время раздачи призов выбирается рандомный победитель с помощью генератора чисел. Таких сервисов в интернете много, их называют рандомайзерами. Принцип пользования очень прост. Каждому участнику конкурса присваивается индивидуальный номер. В рандомайзер вводится общее число участников, после чего программа выдает рандомное число. Победителем считается человек, чей конкурсный номер совпал с числом, выданным рандомайзером.

Это не исключительный вариант использования термина. Слово настолько прижилось, что стало полноправным синонимом слова «случайно». Оно используется и за пределами сети.
Несмотря на давность появления, «рандомно» используется и по сей день. Употребление термина популярно как среди молодежи, так и среди взрослых.
С происхождением и использованием сленговых выражений, таких как: рофлю, страйк, коннект, – можно ознакомиться в других статьях.
Что такое рандом?
Если сказать совсем просто, то рандом — это «случайность».
Если говорить развёрнуто, то «рандом» является англицизмом, то есть происходит из английского языка, есть там такое слово —random, которое можно перевести как «случайный», «произвольный» (два прилагательных), «случайность» (существительное), «наугад», «наудачу» (два наречия). По-другому рандом определяется как «вероятность результата» при совершении каких-либо действий, а ещё «случайно произошедшее событие» и «случайный выбор».
В компьютерных- и онлайн-играх рандом применяется, например, для того, чтобы свести игроков. Точнее сказать, игроки для конкретной, скажем для примера, гонки, подбираются рандомно. Играли в NFS World? Там перед началом гонки с реальными игроками происходит подбор таковых. Подбор этот происходит случайным образом. В шутерах по типу GTA на улицах появляются рандомные прохожие, какой-то особой закономерности обычно нет. Однако вот есть игры, где появление этих прохожих налажено, то есть появляются какие-то определённые лица в зависимости от местности. Это рандомом уже не назвать. Также в шутерах можно встретить выражение «рандомная стрельба» — это обозначает беспорядочную стрельбу, когда игрок особо ни в кого не прицеливается, но стреляет по кому-то.
Сейчас в интернете стали популярны всякие конкурсы, где победителей выбирают с помощью рандомного определителя чисел. Предположим, что в группе проводится конкурс лучших фотожаб. Победитель определяется рандомно с помощью специальных созданных для этого дела сайтов.
Алгоритмы рандома
В этой статье вы увидите самые разнообразные велосипеды алгоритмы для генерации случайных чисел.
Про что статья
C++ rand
Первое что узнаёт начинающий программист С++ по теме получения рандома — функция rand, которая генерирует случайное число в пределах от 0 и RAND_MAX. Константа RAND_MAX описана в файле stdlib.h и равна 32’767, но этом может быть не так, например в Linux (см. коммент). Если же rand() в вашем компиляторе генерирует числа в пределах 32’767 (0x7FFF) и вы хотите получить случайное число большого размера, то код ниже можно рассматривать как вариант решения этой проблемы:
Реализация функции rand в старом C была проста и имела следующий вид:
Данная реализация имела не очень хорошее распределение чисел и ныне в C++ улучшена. Так же стандартная библиотека C++ предлагает дополнительные способы получения случайного числа, о которых ниже.
С++11 STL random
Данный сорт рандома появился в C++11 и представляет из себя следующий набор классов: minstd_rand, mt19937, ranlux, knuth_b и разные их вариации.
Чтобы последовательность случайных чисел не повторялась при каждом запуске программы, задают «зерно» псевдослучайного генератора в виде текущего времени или, в случае с некоторыми ретро (и не только) играми — интервалы между нажатиями клавиш с клавиатуры/джойстика. Библиотека random же предлагает использовать std::random_device для получения зерна лучше чем от time(NULL), однако в случае с компилятором MinGW в Windows функция практически не работает так как надо. До сих пор…
Некоторые из алгоритмов в STL random могут работать быстрее чем rand(), но давать менее качественную последовательность случайных чисел.
PRNG — Pseudo-random Numbers Generator
Можете считать это название — синонимом линейного конгруэнтного метода. PRNG алгоритмы похожи на реализацию rand в C и отличаются лишь константами.
PRNG алгоритмы быстро работают и легки в реализации на многих языках, но не обладают большим периодом.
XorShift
Алгоритм имеющий множество вариаций отличающихся друг от друга периодом и используемыми регистрами. Подробности и разновидности XorShift’а можете посмотреть на Википедии или Хабре. Приведу один из вариантов с последовательностью 2 в 128-й степени.
Данный генератор очень хорош тем, что в нём вообще нет операций деления и умножения — это может быть полезно на процессорах и микроконтроллерах в которых нету ассемблерных инструкций деления/умножения (PIC16, Z80, 6502).
8-bit рандом в эмуляторе z26
Z26 это эмулятор старенькой приставки Atari2600, в коде которого можно обнаружить рандом ориентированный на работу с 1-байтовыми регистрами.
Однажды мне пришлось сделать реализацию этого алгоритма для z80:
Компактный рандом для Z80 от Joe Wingbermuehle
Если вам интересно написание программ под машины с зилогом, то представляю вашему вниманию алгоритм от Joe Wingbermuehle (работает только на зилоге):
Генератор рандома в DOOM
В исходниках игры Дум есть такой интересный файл под названием m_random.c (см. код), в котором описана функция «табличного» рандома, то есть там вообще нет никаких формул и магии с битовыми сдвигами.
Приведу более компактный код наглядно показывающий работу этой функции.
Конечно же это ни какой не рандом и последовательность случайных чисел легко предугадать даже на уровне интуиции в процессе игры, но работает всё это крайне быстро. Если вам не особо важна криптографическая стойкость и вы хотите что-то быстро генерирующее «типа-рандом», то эта функция для вас. Кстати в Quake3 рандом выглядит просто — rand()&0x7FFF.
RDRAND
Некоторые современные процессоры способны генерировать случайные числа с помощью одной ассемблерной команды — RDRAND. Для использования этой функции в C++ вы можете вручную прописать нужные инструкции ассемблерными вставками или же в GCC подключить файл immintrin.h и выбрать любую из вариаций функции _rdrandXX_step, где XX означает число бит в регистре и может быть равно 16, 32 или 64.
Концовка
Класс std::minstd_rand из библиотеки STL random работает быстрее обыкновенного rand() и может стать его альтернативной заменой, если вас не особо волнует длинна периода в minstd. Возможны различия в работе этих функций в Windows и Unix’ах.
Рандомизация в математике и в жизни
Рандомизация (от английского random — случайный) означает сознательное внесение случайного элемента в какой-то процесс. Когда-то люди, решавшие, как им быть, подбрасыванием монеты или вытаскиванием спичек, почитались за несерьезных. Но теперь пора заняться их реабилитацией: строго доказано, что многие важные задачи требуют для решения бросать жребий. Отвлечемся пока от спортивных страстей далекого прошлого и послушаем ученых.
Теория игр
В 1921 году французский математик Эмиль Борель опубликовал статью, которая в то время никого не заинтересовала. Даже Иоганна фон Неймана, в будущем знаменитого, а тогда еще безвестного немецкого юношу, который пятью годами позже выступил на ту же тему перед собранием Геттингенского математического общества. А в 1943 году тот же фон Нейман, ставший к тому времени из Иоганна Джоном, вместе с другим американским ученым, О. Моргенштерном, опубликовал книгу «Теория игр и экономическое поведение». Один пример из неё стоит того, чтобы его привести здесь. Он относится к столкновению между Шерлоком Холмсом и профессором Мориарти.
Напомним, что Шерлоку Холмсу пришлось бежать из Лондона от своего неумолимого врага в Дувр и дальше во Францию. Но успех бегства с самого начала оказался под вопросом: отъезжая, на перроне в Лондоне Холмс увидел Мориарти, и ему стало ясно, что неизбежна погоня на специальном поезде. У Холмса были две возможности: ехать все же до Дувра или высадиться в Кентенберри, единственном промежуточном пункте, где поезд делал остановку. Те же две возможности были и у его преследователя. Какое решение должны принять оба участника конфликта?
Прежде всего, нужна какая-то количественная мера происходящего, которую Нейман и Моргенштерн предлагают установить, так. Если Холмс высадится в Кентенберри и Мориарти тоже, то это будет для Мориарти стопроцентная удача, как и случай, если оба попадут в Дувр. Если Холмс прибудет в Кентенберри, а Мориарти в Дувр, то это будет ничья (то есть выигрыш Мориарти составит 0 процентов), ибо и цель Холмса — попасть во Францию — не будет достигнута. Наконец, если Мориарти высадится в Кентенберри, а Холмс доедет до Дувра и ускользнет, то преступник будет посрамлен, что авторы оценили в половину стоимости жизни Холмса (стоимости для Мориарти), то есть в виде выигрыша в 50 процентов. Примем указанные числа как непреложные и зададимся вопросом: как должен поступать мудрый, но, увы, не всесильный Холмс, чтобы его шансы остаться в живых были максимальными? И как действовать Мориарти, чтобы добиться успеха?
По Нейману и Моргенштерну, решение задачи таково: обоим участникам конфликта следует рандомизировать свое поведение. Мориарти должен с вероятностью 3/5 оказаться в Дувре, а с вероятностью 2/5 в Кентенберри. Холмс, наоборот, с вероятностью 3/5 в Кентенберри и 2/5— в Дувре. Но как практически реализовать эту рекомендацию?
Понятно, что если бы погоня происходила 100 раз, то Холмсу надо было высаживаться в Кентенберри 60 раз, но так, чтобы Мориарти каждый раз был в неведении относительно его планов. Однако даже великие сыщики располагают только одной жизнью. И как действовать Мориарти, чтобы реализовать свои шансы? К примеру, вот как. Он может взять круглую палочку и выстругать на ней пять одинаковых граней (вряд ли злодей выходит из дому без ножа). Три из граней Мориарти должен пометить крестиками и бросить палочку на перрон. Если палочка упадет на помеченную грань, то Морирати должен ехать до Дувра, а если на чистую — до Кентенберри. В свою очередь Холмс должен пометить только две грани, а в остальном поступать так же.
Счастливая замена одного наилучшего решения многими, которые следует применять с оптимальными частотами,— это, на наш взгляд, одно из главных достижений математики в наше время. И самое поразительное, если одна из сторон уклонится от такого образа действий, то она даст противнику дополнительные шансы на успех. Это сумели показать Борель и другие, и тут сильная сторона их подхода. А слабые стороны? Они есть? К сожалению, да.
Начнем с того, что веские соображения о числах, которые Нейман и Моргенштерн приняли равными 100, 0 и 50, начинаются обычно со стыдливого «допустим». Действительно, и в ситуации из рассказа, и в многочисленных экономических и военных предположениях теории игр исследователи неизбежно наталкивались на отсутствие необходимых количественных характеристик.
Теория игр развивалась интенсивно. Она умеет уже описывать случаи, когда участников конфликта не два, а сколько угодно. Даже когда их бесконечно много. Более того, участники конфликта могут вступать, в коалиции друг с другом так, чтобы их интересы в чем-то совпадали. Но всегда остается справедливым такой вывод: если игра не содержит никакой неопределенности, если это игра «с полной информацией», то наилучшее решение в каждой ситуации строго определенной не нуждается в рандомизации. И наоборот, если в игре есть элемент неопределенности (к примеру, вносимый противником), то наилучшее решение носит в общем случае случайный, рандомизированный характер.
Мы обсудили вслед за Нейманом и Моргенштерном случай, когда выбор носил дискретный характер — Кентенберри или Дувр. Но ничто не мешает теперь включить в рассмотрение любой ярд дороги Лондон — Дувр. Если Холмс легко гнул железную кочергу, то и прыжок с поезда был ему, вероятно, по плечам (или по ногам). Но тогда этот шанс пришлось бы оставить и за коварным Мориарти. В таком случае мы получаем задачу не дискретных, а «дифференциальных игр». Этот термин ввел американский ученый Р. Айзеке, причем основное внимание он уделил именно задачам преследования. Кто только за кем ни гоняется в книге Р. Айзекса «Дифференциальные игры»!
Шофер за пешеходом, катер за кораблем, футбольный защитник за нападающим, снаряды за самолетами и даже… чудовище за принцессой! Любопытна формулировка последней задачи. Чудовище ищет принцессу в абсолютно темном помещении. Поимка происходит тогда, когда расстояние между ними станет меньше заданного. Известна максимальная скорость чудовища, а скорость принцессы может быть любой. Какими должны быть стратегии бедняжки и ее мучителя? Р. Айзеке признается, что решение задачи ему неизвестно, но он полагает, что оно должно быть рандомизированным. Действительно, для принцессы обе крайности — стоять на месте или двигаться с огромной скоростью — явно не сулят ничего хорошего. Несмотря на леденящие душу условия задачи, судьба несчастной пока не подвинула ни одного ученого на ее решение.
Постепенно обнаружилось, что рандомизация имеет смысл и тогда, когда, по идее, вся информация имеется. Классическим примером могут служить шахматы. Положение всех фигур на шахматной доске известно обоим противникам. И значит, в каждой позиции можно (в принципе можно!) указать ход, который приводит к выигрышу за минимальное число ходов (или, скажем, к проигрышу за максимальное, если позиция хуже). Но то, что возможно в принципе, отнюдь не всегда осуществимо технически. Совершенно немыслимое количество позиций, которые могут возникнуть в шахматной партии, делают абсурдом попытку рассмотреть их все полностью. И в основу шахматных программ часто закладывают метод случайного поиска — рандомизированный метод отыскания оптимального решения. Поясним сущность этого метода на примере.
Случайный поиск
Допустим, мы хотим подобрать параметры электродвигателя, которые делают его наиболее экономичным при всех режимах работы. Зависимости, связывающие эти параметры с переменными, характеризующими условия работы электродвигателя, нам известны. Однако они слишком сложны, чтобы непосредственно судить, какими выбрать оптимальные параметры. Можно назначить наугад несколько тысяч наборов и выбрать из них наилучший — это так называемый слепой случайный поиск. И здравый смысл, и вычислительная практика говорят, что такая стратегия не ведет к успеху. Необходимо ввести элементы самообучения, чтобы компьютер в процессе поиска учитывал накопленный опыт. К примеру, таким путем – вести поиск сериями.
Первая серия испытаний возможных параметров проводится описанным образом. Во второй серии чаще испытываются те точки, которые показались наиболее экономичными после первой серии испытаний. Скорее всего, это позволит найти еще лучший набор параметров. Тогда на следующей серии испытаний проверяемые точки ложатся еще кучнее по отношению к новым оптимальным — признак того, что полученной информации о наилучших значениях параметров можно доверять. И наоборот, если очередная серия испытаний не дала улучшения, то разброс исследуемых точек вокруг оптимальных значений можно увеличить — неудачный результат серии приводит к понижению нашего доверия к полученной информации. И так до тех пор, пока исследуемые точки не станут сливаться в одну. Это признак того, что поиск можно остановить.
А вот другой способ самообучения. Улавливают тенденцию в изменении параметров двигателя, при которой повышается его экономичность, а затем выясняют, до каких пор эта тенденция сохраняется. Добравшись до этого места, снова выявляют тенденцию и так далее. Но как выбрать благоприятную тенденцию изменения? А все так же, перебирая возможные случайным образом.
Существует много разнообразных идей самообучения в методах случайного поиска, но суть всех этих методов одна и та же: они ставят целью преодолеть нехватку информации о поведении исследуемого объекта. И если считать, что объект старается скрыть от нас свои тайны и сознательно мешает найти наилучшие параметры, то такой путь с точки зрения теории игр является оправданным.
«Но позвольте,— возразят тут многие читатели,— ведь здесь речь идет не о хитроумном Мориарти, а всего лишь об электродвигателе, который вряд ли враждебен нам и отнюдь не старается помешать выявлению своих оптимальных параметров». И действительно, оптимизация электродвигателя — это вовсе не конфликтная ситуация с неполной информацией. Однако выясняется, что электродвигатель удобно наделить свойствами мыслящего противника, чтобы построить эффективный (хотя и не оптимальный) алгоритм поиска оптимальных параметров. Впрочем, на этот счет еще ведутся споры.
Планирование экспериментов
Один из разделов науки, в которых необходимость рандомизации признается всеми специалистами,— планирование экспериментов. Допустим, мы ищем наилучший сорт пшеницы для данного района. Для этого в течение нескольких лет в разные сроки засевается несколько участков. Если назначать участки под пшеницу, руководствуясь какими-то рациональными правилами, то где гарантия, что мы не «подыграем» тому сорту, которому симпатизируем, назначив ему лучший участок? Или не обречем на провал другой сорт только потому, что нам почему-либо не понравилось его название? Вы скажете, что постараетесь быть объективным,— напрасные старания! Пытаясь поступать вопреки своим предпочтениям, вы впадаете лишь в противоположную крайность, и результаты ваших экспериментов все равно не будут объективными.
Только рандомизация способна обеспечить объективность эксперимента. К сожалению, известно немало случаев, когда экспериментатор был уверен в своей объективности и не замечал, что вносит в подготовку эксперимента условия, искажающие его результат.
Классический пример такой ошибки — предсказание результатов выборов президента США в 1936 году, когда им стал Ф. Д. Рузвельт. Экспериментатор опрашивал избирателей по телефону и не учел, что в то время владельцы телефонов отражали мнение лишь наиболее обеспеченных граждан. Большинство владельцев телефонов действительно голосовало против Рузвельта, в то время как большинство всего населения — за него. Правильный эксперимент заключался бы в случайном выборе кандидатур для опроса из полного списка избирателей.
На первый взгляд мотивы, которые побуждают к рандомизации в теории решений и в планировании экспериментов, существенно разнятся. Но на самом деле эти различия не столь уж значительны. Ибо истоки рандомизации те же — нехватка информации. Если бы мы были уверены, что владеем точными физическими законами и точно проводим измерения, то для определения оптимальных параметров понадобилось бы не больше экспериментов, чем этих параметров. В частности, если бы избиратели действовали как один человек, то достаточно было бы опросить лишь одного американца (любого!) Нелепость такого подхода совершенно очевидна.
Статистическое моделирование
Мы коснулись роли рандомизации в экспериментах над некоторыми физическими, биологическими или социальными объектами. Но эксперимент может проводиться и с математической моделью объекта. Как поведет себя телефонная станция, если разговоры абонентов будут преимущественно короткими и частыми? Как, если редкими, но долгими? На все эти вопросы нетрудно ответить с помощью экспериментов над действующей телефонной станцией. А что делать, если эта станция только проектируется? Тут приходит на помощь статистическое моделирование.
В математическую модель станции посылаются случайные «звонки» и находится ее реакция. Статистическая модель станции — это всего лишь программа для компьютера, стоит она неизмеримо меньше настоящей станции — семиэтажного здания, набитого всяческим оборудованием. И, тем не менее, такая модель способна дать ответ на вопрос, что ждет клиента, которому срочно понадобится скорая помощь или участливая трепотня приятеля. Соединится ли он с интересующим его объектом за минуту? А за две? И ответы эти можно получить не за год эксплуатации станции, а всего лишь за несколько минут: ведь компьютер позволяет сжимать время. Набор номера, который даже натренированная рука проводит за двадцать секунд, компьютер генерирует за десятитысячную долю секунды.
И тут тоже использование рандомизированной информации на входе неизбежно: нет строгих законов, которые регламентировали бы наше желание кому-то позвонить. А опираясь на какие-то детерминированные допущения, мы неизбежно исказим результаты исследования.
Счастливый случай
Обращение к случаю стало счастливой находкой для многих исследователей. Эпидемия рандомизации охватывает все новые разделы техники, экономики,- социологии. Ученых привлекает почти ничем не ограниченная свобода творчества, отсутствие строгих канонов, порой стесняющих воображение в иных подходах. Иногда, благодаря этой свободе, дело доходит до более или менее полного абсурда. К примеру, один австралийский исследователь предложил случайным образом вводить армирование в железобетонных конструкциях. Дескать, все равно нам не известны в точности законы, связывающие прочность с армированием, как неизвестен и критерий качества железобетонной конструкции. Его коллега, едко возражая против этого подхода, заметил, что логическим развитием такого метода должна быть рандомизация в медицине: поскольку неизвестны причины многих болезней, а диагнозы далеко не всегда точны, то можно рекомендовать врачу после осмотра больного случайным образом брать лекарство с полки.
Но даже если закрыть глаза на крайности, которыми богата современная жизнь науки, то следует признать, что не все ученые разделяют идеи рандомизации в теории решений. Многие заявляют, что лучше уж вкладывать в математические модели самые несовершенные, но зато детерминированные механизмы, чем полагаться на волю слепого (или пусть даже только подслеповатого случая). Это сродни спорам, которые велись в двадцатые годы прошлого века относительно статистических методов в физике. Тогда А. Эйнштейн заявлял, что он не верит, будто Бог, прежде чем назначить положение электрона, бросает кости. Тем меньше оснований, заявляют современные противники рандомизации, заниматься этим малодостойным делом человеку. Человек должен стараться постигнуть законы бытия, устранить белые пятна, а не прятаться от них в скорлупу рандомизации.
По обличью этот призыв вроде бы здрав, а по сути не очень. Слишком долго считалось, что научный подход — это нечто противоположное ненадежной игре случая. Трудно отрешиться от этого представления и уверовать, что сам случай может быть вставлен в оглобли, использован в качестве тягловой силы науки. Но пока еще Случай нередко брыкается…
Спинтакс — что это такое? Делаем рандомизацию текста правильно!
Автор: Игорь Кантор · Опубликовано 12 апреля, 2020 · Обновлено 29 октября, 2021
Главная > Теория и практика > Спинтакс — что это такое? Делаем рандомизацию текста правильно!
Всем привет! С вами Игорь Кантор и я хотел бы кратко рассказать о такой важной вещи, как рандомизация текста. Многие мои подписчики рандомизируют тексты каждый день или заказывают подобные услуги у фрилансеров (об этом в конце). В статье речь пойдет про спинтакс, о том, как его правильно составить и какие инструменты могут нам в этом помочь. Поехали!
Для чего нужна рандомизация текста
Рандомизация текста, в основном, востребована у вебмастеров (услуги копирайтинга/рерайтинга), но часто, ей не брезгуют и арбитражники для решения своих повседневных задач. Понятное дело, рандомизация вряд ли может быть связана с честным продвижением. Если вы ведете «белоснежный» бизнес в сети, то, возможно, вам никогда не придется прибегать к этому. Но, реальность такова, что приходится)
Рандомизация текста — это генерация большого кол-ва уникальных комбинаций, путем замены слов или фраз на синонимы, а также, перестановки их местами. На выходе мы получаем ту же смысловую нагрузку, но описанную разными словами.
Основные направления, где требуется генерировать рандомизированные тексты:
Необходимость в уникализации вызвана, прежде всего, спецификой поисковых роботов и антиспам алгоритмами. Поисковые системы заботятся о релевантной выдаче и не будут продвигать ресурс с дублирующим контентом.
Алгоритмы соцсетей, при малейшем подозрении на неуникальность рассылаемых текстов банят аккаунты за спам. Те, кто уже работал по этой или по этой схемам, знают об этом не по наслышке)
Расскажу, как обычно делается рандомизация для рассылок. Если вы занимаетесь SEO, то подход будет аналогичным, за исключением бОльших объемов текста.
Что такое спинтакс?
Спинтакс — это специальный метод генерации рандомизированных текстов. Большинство приложений и инструментов, работающих с уникализацией текстов договорились использовать такой формат. Синтаксис спинтакса следующий:
При вводе такой конструкции рандомизатор на выходе выдает 3 уникальных варианта текста: «a» «b» или «c». Алгоритм случайным образом берет одно из значений в фигурных скобках. Синонимы отделяются знаком «|».
Большинство инструментов (если не все) по рандомизации текстов работают с форматом «спинтакс»
Все очень просто, правда? Добавляя следующий блок из фигурных скобок мы получаем все возможные пересечения между случайным словом/фразой/предложением из первого блока скобок со вторым блоком скобок:
На выходе получим 4 уникальных комбинации:
Расширенный спинтакс
Некоторые инструменты позволяют работать с расширенным синтаксисом спинтакса. Он дополняет стандартный следующими конструкциями:
В данном случае, будет выполнена случайная перестановка значений. На выходе получим следующие варианты:
abc acb bac bca cab cba
Следующая конструкция позволяет добавлять символ-разделитель в функцию перестановки:
Символ, указанный между ++ будет помещен в качестве разделителя между переменными в перестановку (для экранирования спецсимволов применяется знак \). В результате рандомизации будут сгенерированы следующие варианты перестановок:
a,b,c a,c,b b,a,c b,c,a c,a,b c,b,a
Еще одна возможность расширенного спинтакса — поддержка вложенности конструкций:
ВАЖНО! Далеко не все инструменты поддерживают расширенный спинтакс. Будьте внимательны и проверяйте возможности софта, который вы применяете.
Например, один из инструментов, который я использую для продвижения в ВКонтакте — не поддерживает вложенные конструкции и перестановки!
Рекомендации по применению спинтакса
Так как в блоге я достаточно подробно освещаю вопрос условно-бесплатного трафика, то и основное применение спинтакса ориентирую под эти задачи. Если для вас актуальны вопросы рассылок в соцсетях автоматизированным способом, то от себя могу порекомендовать следующее:
1. Рандомизация отдельных слов работает лучше рандомизации целых предложений
Такой вариант, с точки зрения банов, работает гораздо лучше:
2. Выносите знаки окончания предложений в отдельный блок <>
Добавляйте разные варианты окончаний, чтобы сделать текст еще более уникальным для алгоритмов антиспама:
3. Используйте конструкции с пропуском слов, вида
Такой подход тоже работает и позволяет разнообразить текст:
Хочу поприветствовать <|всех>своих подписчиков
Главное, что нужно понимать — любой шаблон со временем перестает работать. Если вы встали на такой непростой путь продвижения, как рассылки, будьте готовы много работать с рандомизацией текста.
Генераторы рандомизированного текста
Существует достаточно много сервисов, позволяющих упростить работу по уникализации текста. Среди них есть, как десктопные решения, так и онлайн инструменты. Лично мне, более предпочтительны онлайн сервисы, т.к. я работаю с разных машин и с разными операционками.
В качестве неплохого варианта могу порекомендовать онлайн генератор спинтакс — SeoGenerator:
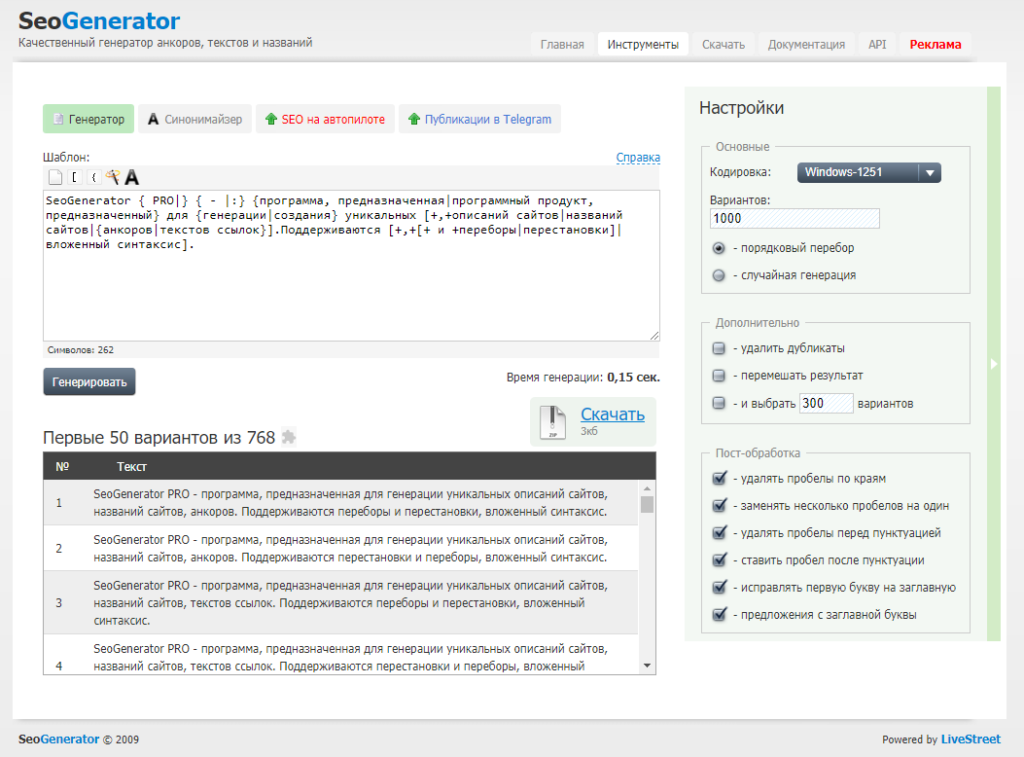
Функционала данного сервиса более, чем достаточно:
Для себя, не вижу поводов искать что-то другое. К тому же, сервис бесплатный.
Заказ услуги на фрилансе
Как я уже говорил, рано или поздно, схема перестает работать. Когда шаблон выгорает, приходится придумывать новый. Чтобы текст оставался привлекательным для целевой аудитории, нужна очень качественная рандомизация. И, честно скажу, не всегда хочется этим заниматься)
Когда одолевает лень или серьезно поджимает время, можно обратиться к профессионалам. На биржах фриланса достаточно специалистов рерайтеров, которые готовы за небольшое вознаграждение рандомизировать любой текст в формате спинтакс. Я, обычно, публикую задание на FL.ru. Довольно быстро находится исполнитель. Если сработаетесь, то потом можно с ним сотрудничать на постоянной основе.
Надеюсь, после прочтения статьи у вас поднимется скилл рандомизации текста и станет меньше банов) Если есть советы или рекомендации по другим инструментам, которыми вы пользуетесь для рандомизации текста — делитесь в комментариях. Думаю, всем будет полезно.
Если работаете страфиком или хотите зарабатывать на партнерках — обязательно ознакомьтесь с материалами по условно-бесплатному трафику из ВК.
С вами был Игорь Кантор, подписывайтесь на мою группу в ВК и канал в Телеграм, чтобы не пропустить свежие схемы. Всем профита и пока!




