Decomposition book что это

Антипаттерны проектирования: Functional Decomposition

Наименование: Functional Decomposition (функциональная декомпозиция)
Другие наименования: No Object-Oriented AntiPattern «No OO»
Масштаб: приложение
Рефакторинг: объектно-ориентированный реинжиниринг

Функциональная декомпозиция — хорошая практика процедурного программирования, так как она позволяет разделить приложение на отдельные функциональные модули.

К сожалению функциональную декомпозицию невозможно напрямую отразить в иерархии классов и поэтому иногда возникают проблемы, описываемые в статье.

Зачастую антипаттерн проявляется, когда опытные в процедурном программировании разработчики начинают проектировать и реализовывать программу на объектно-ориентированном языке. Если разработчики привыкли к наличию главной подпрограммы, которая вызывает другие подпрограммы, то они склонны выполнить каждую подпрограмму в виде класса, полностью игнорируя при этом иерархию классов (и в целом объектно-ориентированный подход).

Результирующий код похож на конструкции структурного языка программирования, реализованные в виде классов. Такой код может быть невероятно сложным, так как опытные разработчики могут придумывать хитрые способы повторить в объектно-ориентированной архитектуре оправданные временем техники процедурного программирования.

С антипаттерном зачастую можно столкнуться, когда С-программист начинает писать на C++, или пытается подключить CORBA интерфейсы, а также пытается использовать какую-либо объектную технологию. В долгосрочной перспективе порой бывает проще нанять программистов с объектно-ориентированным мышлением, нежели тратить время на обучение объектно-ориентированным технологиям.

Признаки появления и последствия антипаттерна

Типичные причины

Исключения

Функциональная декомпозиция приемлема, если не требуется объектно-ориентированного решения. Данное исключение также может быть применено в тех случаях, когда в сущности чисто функциональное решение обернуто в классы для того, чтобы предоставить объектно-ориентированный интерфейс.

Рефакторинг

Если все еще возможно определить изначальные основные требования к ПО, то необходимо сооздать аналитическую модель ПО, которая бы описывала наиболее важные возможности ПО с пользовательской точки зрения. Это очень важно для определения назначения большинства программных конструкций в кодовой базе. На всех этапах рефакторинга антипаттерна необходимо детально документировать вносимые изменения — это облегчит жизнь тем, кто в будущем будет сопровождать систему.

Далее создайте модель проектирования, которая включает основные части существующей системы. Фокусируйтесь не на улучшении модели а на создании основы для описания как можно большей части системы.

В идеальном случае модель проектирования оправдает наличие большинства программных модулей. Разработка модели проектирования существующей кодовой базы очень важно — процесс дает понимание того, как система функционирует в целом.

Пример

Основой функциональной декомпозиции является последовательный вызов функций, выполняющих манипуляцию данными, например с использованием методов структурированного программирования Джэксона (Jackson Structured programming — JSP). Функции зачастую являются методами в объектно-ориентированном контексте. Распределение функций основывается на разных парадигмах ООП, которые приводят к разному группированию функций и связанных с ними данных в классах.

Источник

Создание и просмотр визуальных элементов дерева декомпозиции в Power BI

область применения: ✔️ Power BI Desktop ✔️ службы Power BI

Визуализация в виде дерева декомпозиции в Power BI позволяет визуализировать данные в нескольких измерениях. Она автоматически выполняет статистическую обработку данных и позволяет детализировать измерения в любом порядке. Это визуализация искусственного интеллекта (ИИ), которая может искать новые измерения для выполнения детализации на основе определенных критериев. Она выступает ценным инструментом для специализированного изучения и проведения анализа первопричин.

В этом учебнике используются два примера:

PBIX-файл, используемый в сценарии цепочки поставок, можно найти здесь: PBIX-файл примера цепочки поставок.

Для предоставления общего доступа к отчету Power BI и вам, и коллеге необходимо иметь отдельные лицензии Power BI Pro или сохранить отчет в емкости Премиум.

Начало работы

Выберите значок дерева декомпозиции в области «Визуализация».

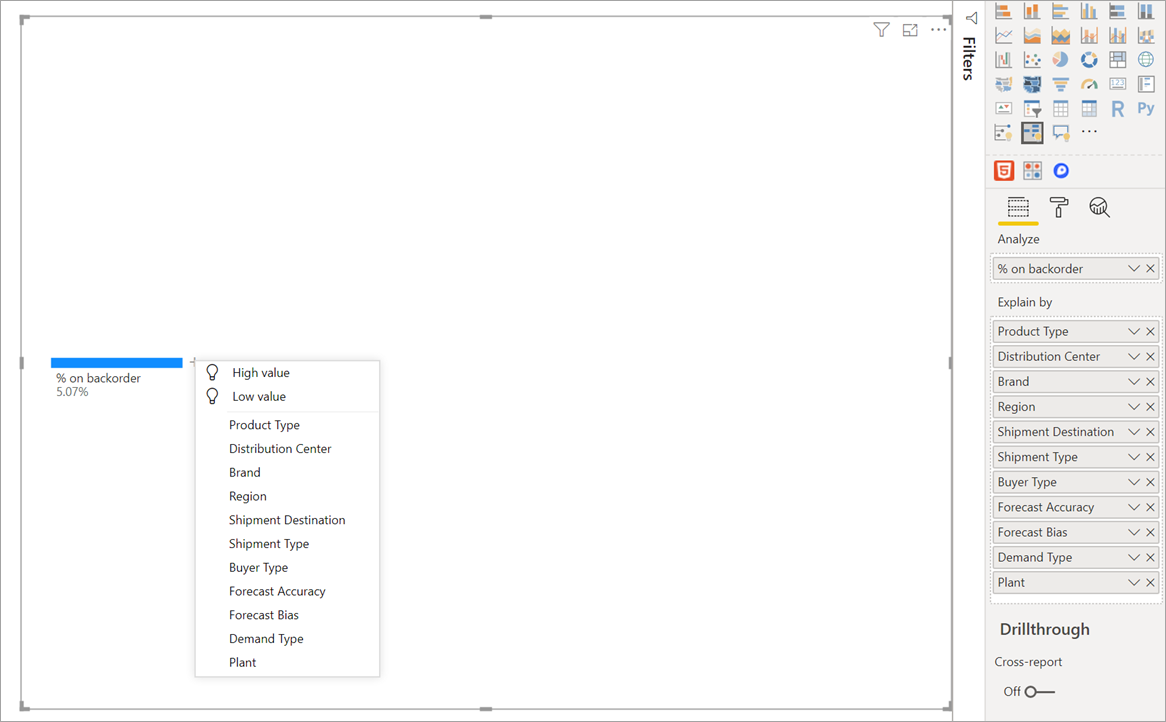
Для визуализации требуется два типа входных данных.

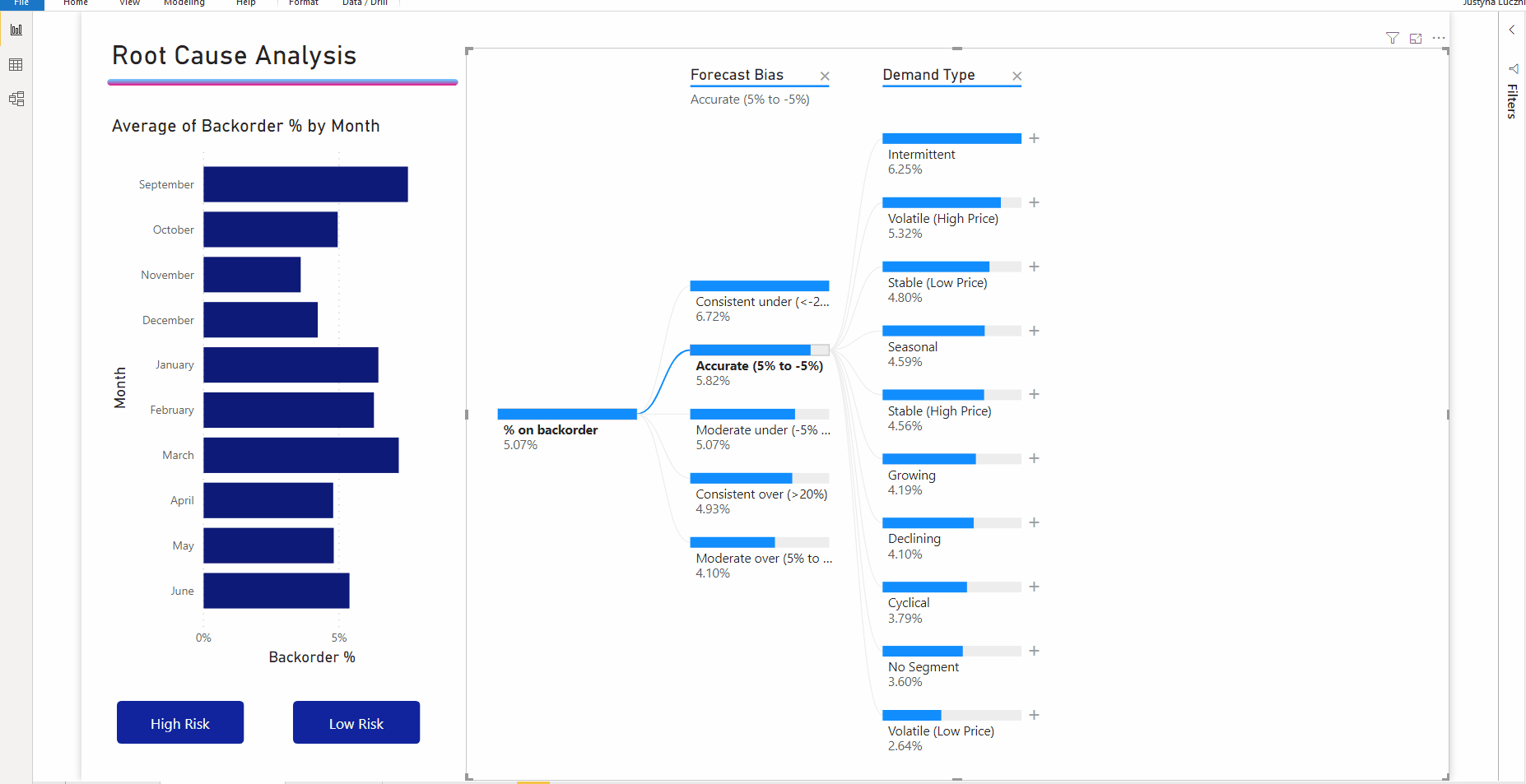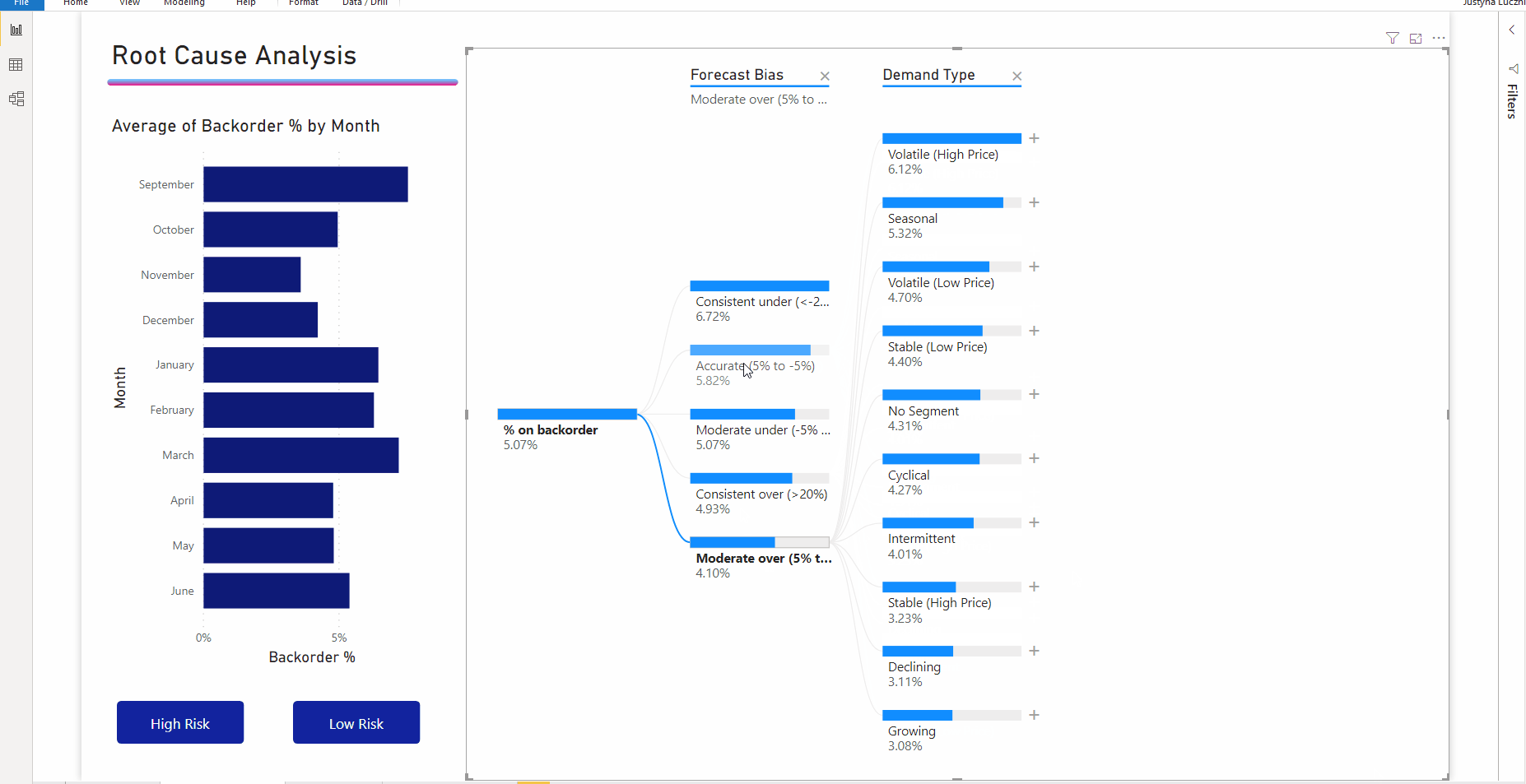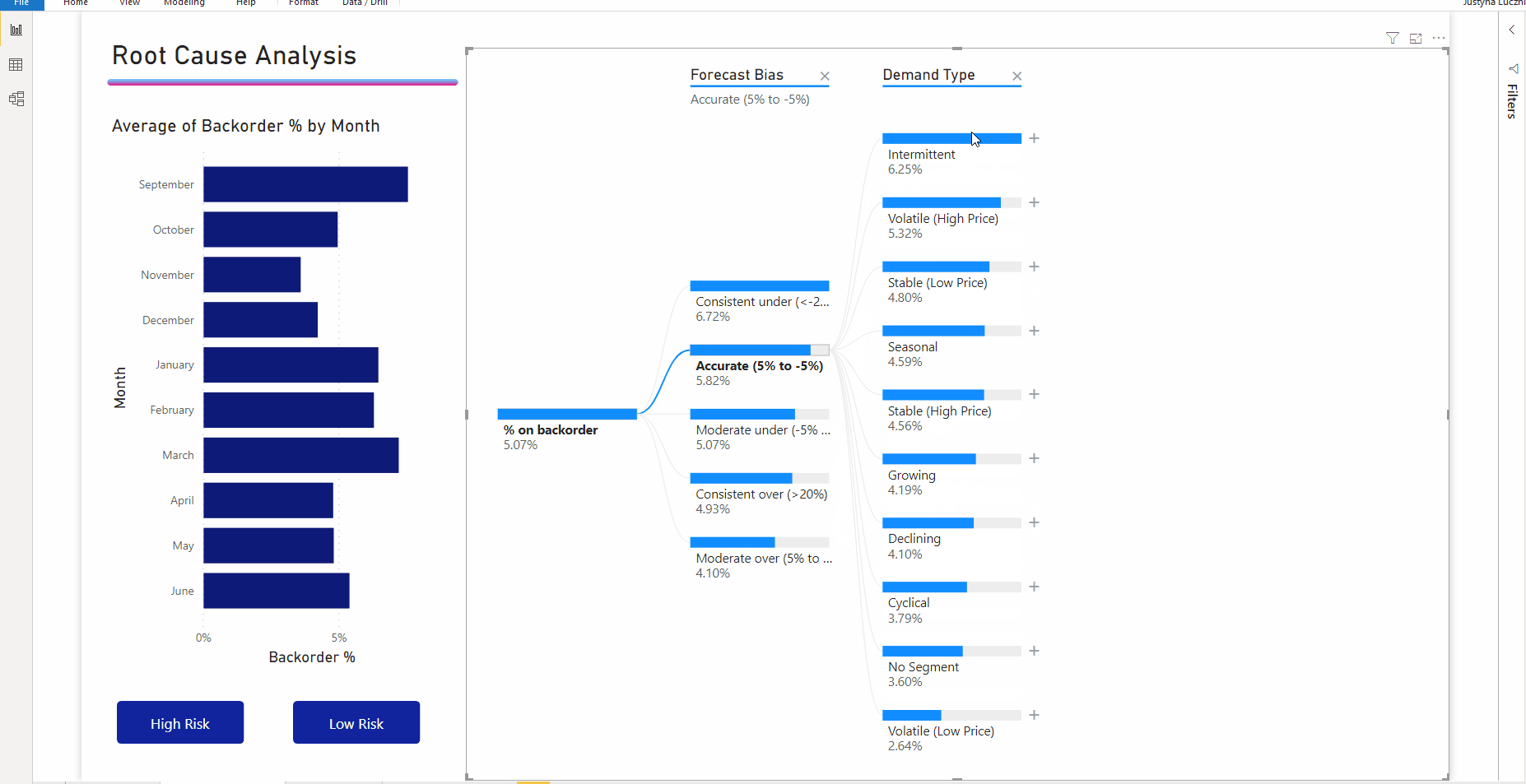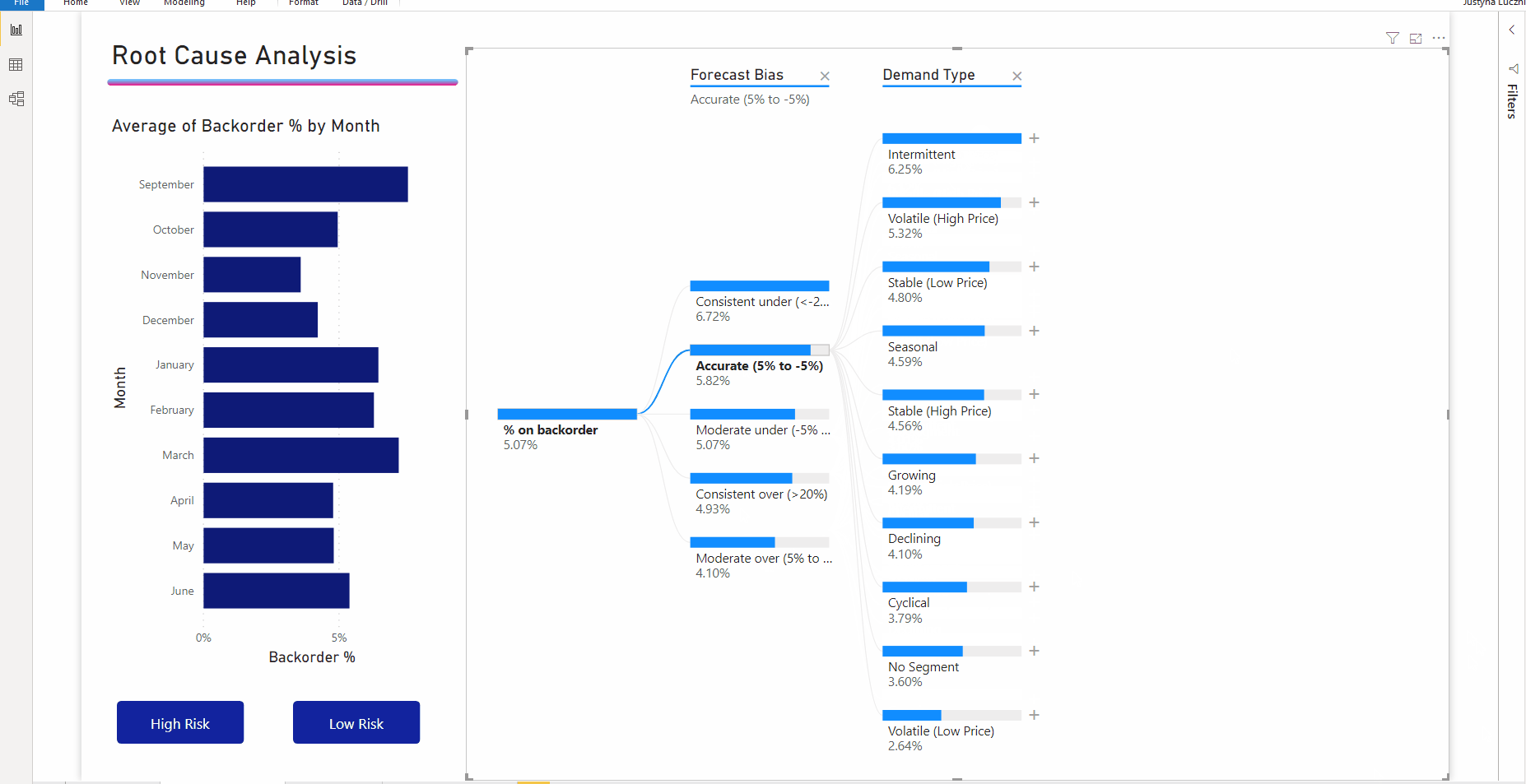
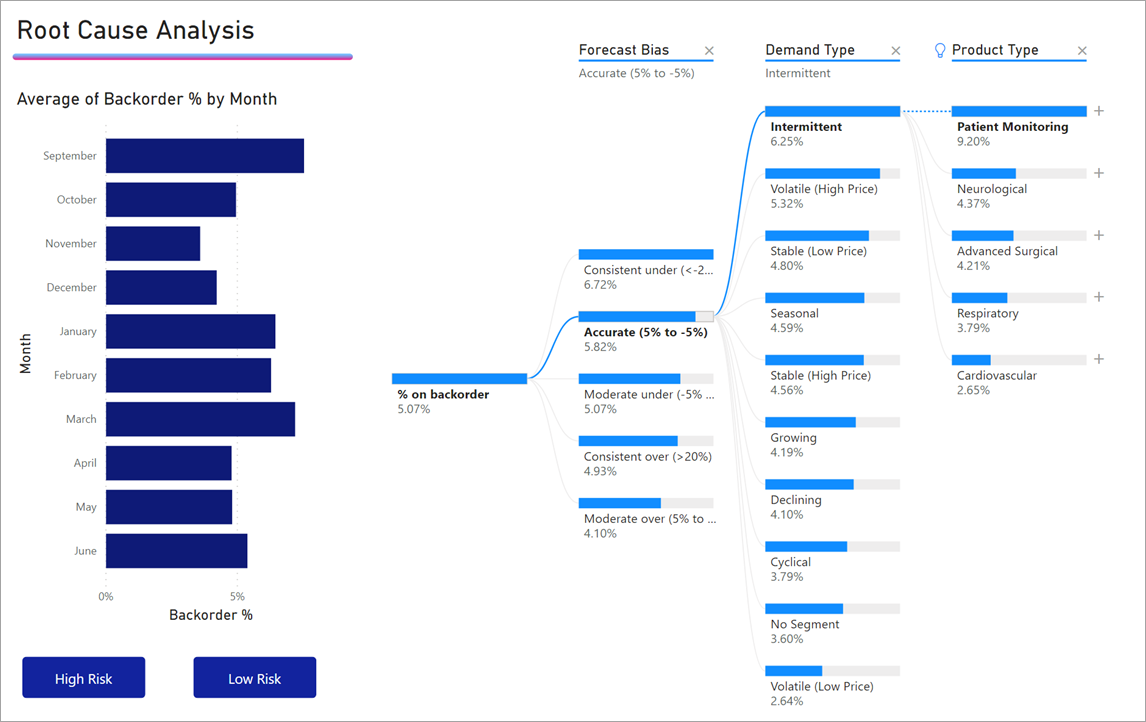
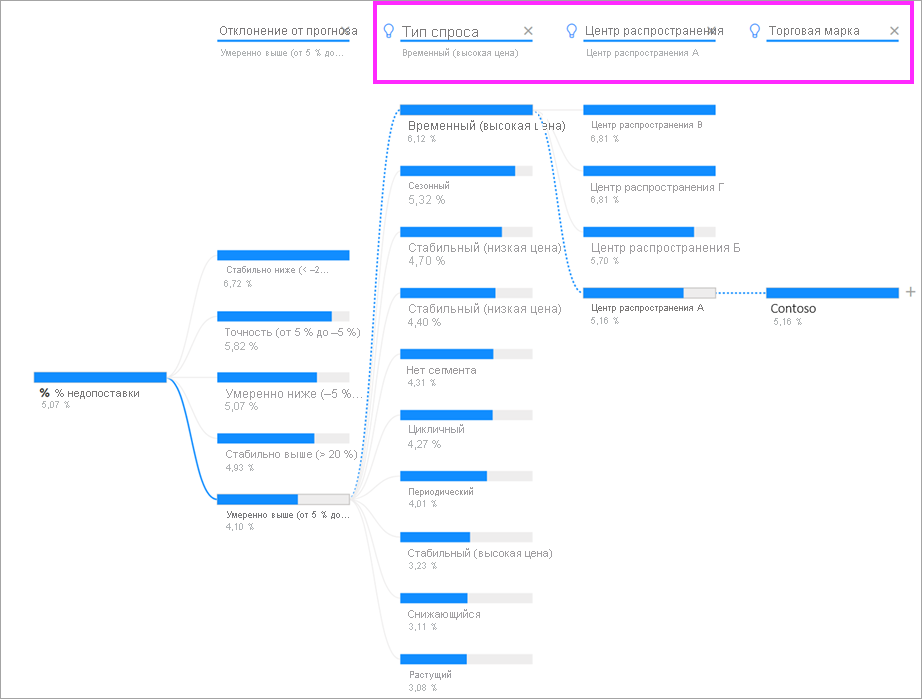
После перетаскивания меры в область полей визуальный элемент обновится и отобразит агрегированную меру. В приведенном ниже примере мы будем визуализировать средний процент продуктов, которые требуется дозаказать (5,07 %).

Далее требуется выбрать одно или несколько измерений, для которых необходимо выполнить детализацию. Добавьте эти поля в контейнер Объяснение по. Обратите внимание, что рядом с корневым узлом отображается знак «плюс». С помощью знака «плюс» можно выбрать, для какого поля нужно выполнить детализацию (вы можете детализировать поля в любом порядке).

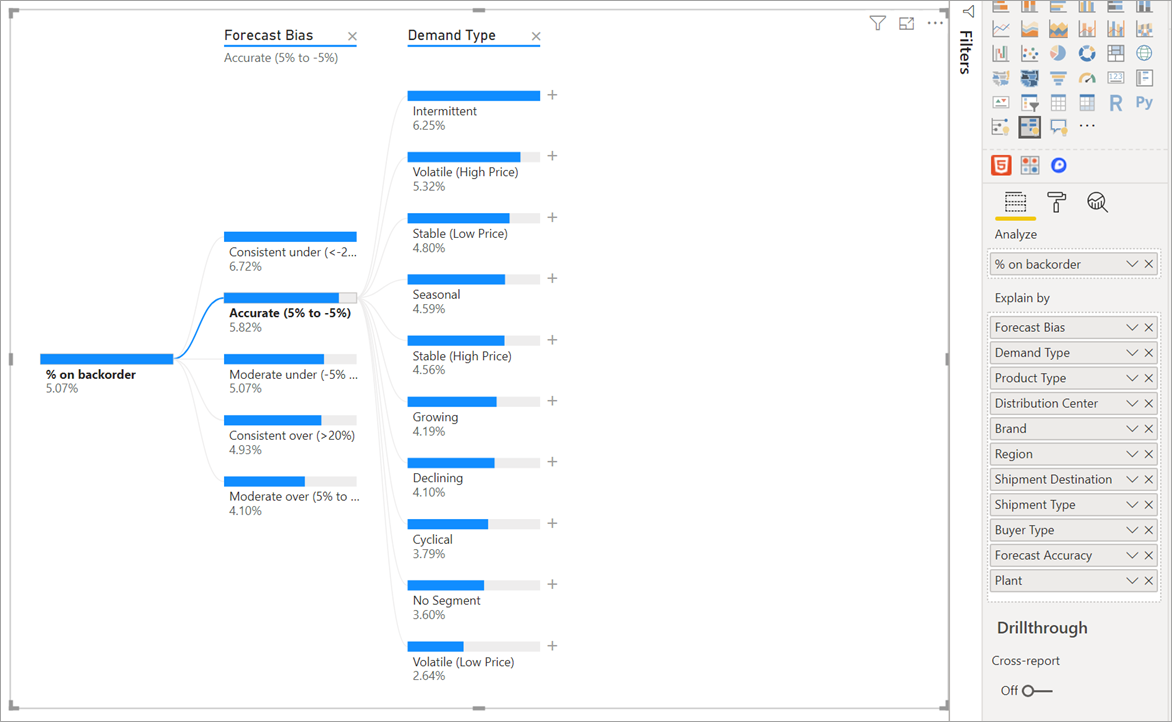
Щелкните Forecast bias (Смещение прогноза), чтобы развернуть дерево и разбить меры по значениям в столбце. Этот процесс можно повторить, выбрав другой узел для детализации.

Если выбрать узел из последнего уровня, будет выполнена перекрестная фильтрация данных. Выбор узла на более раннем уровне приведет к изменению пути.

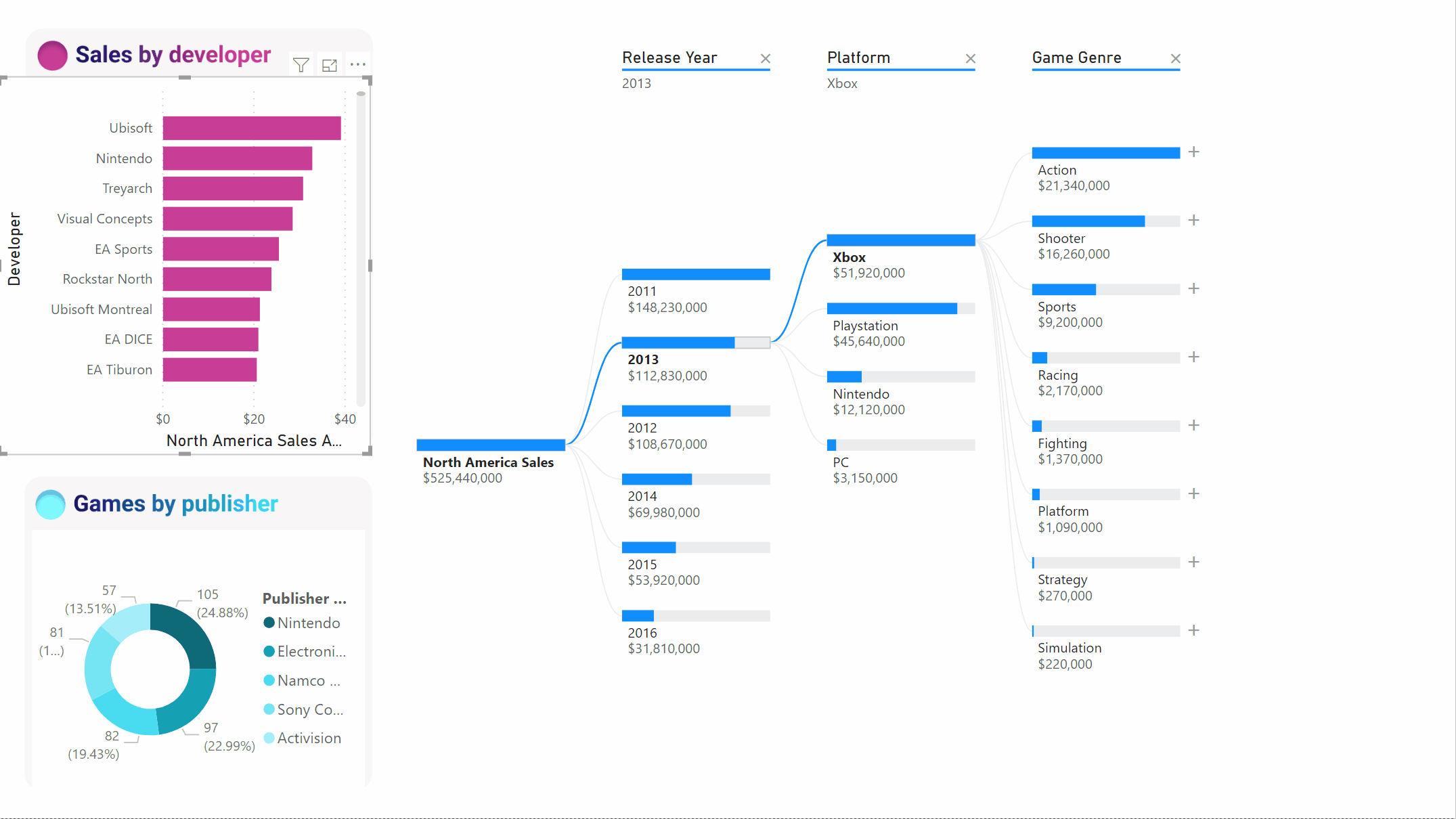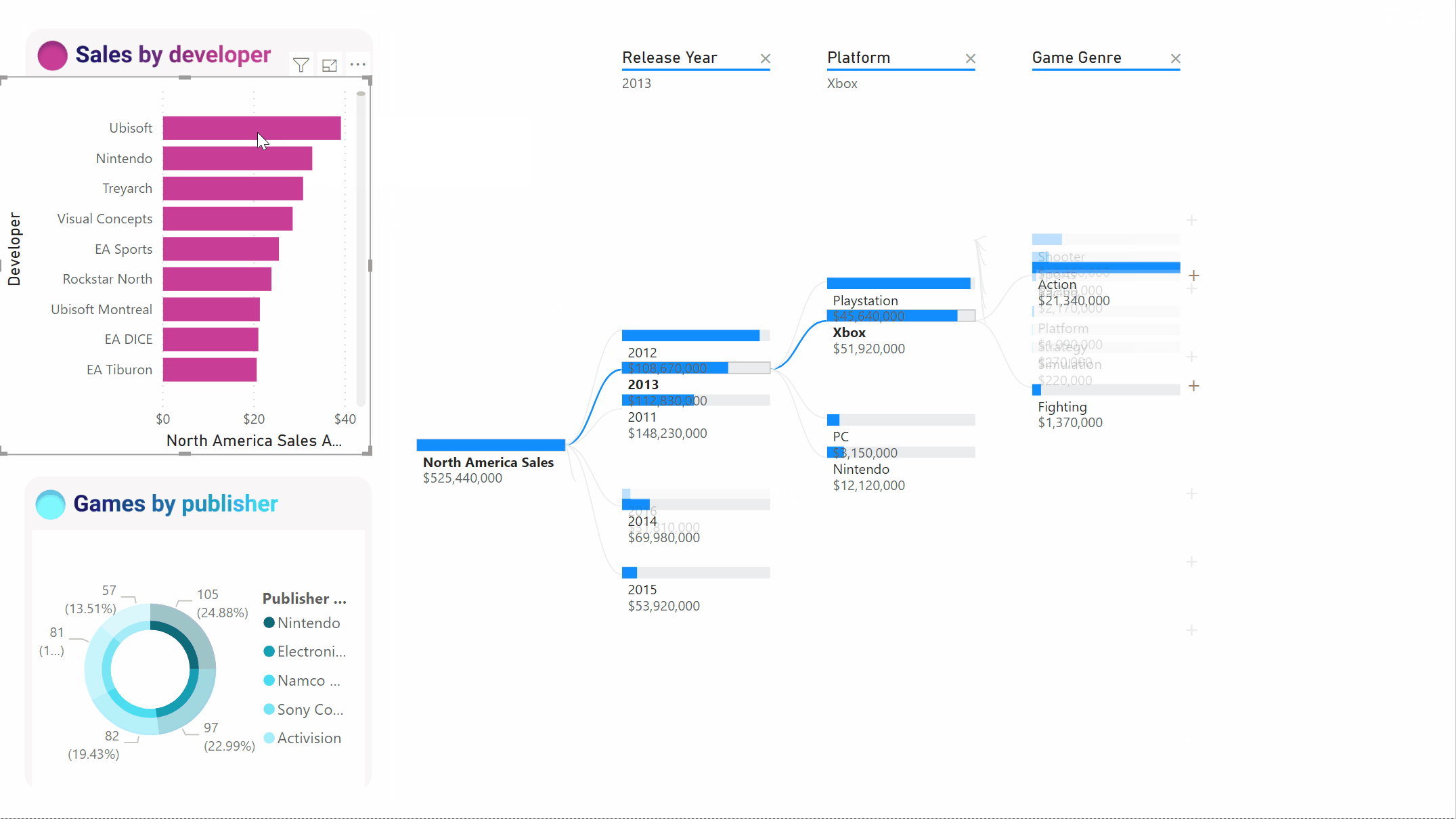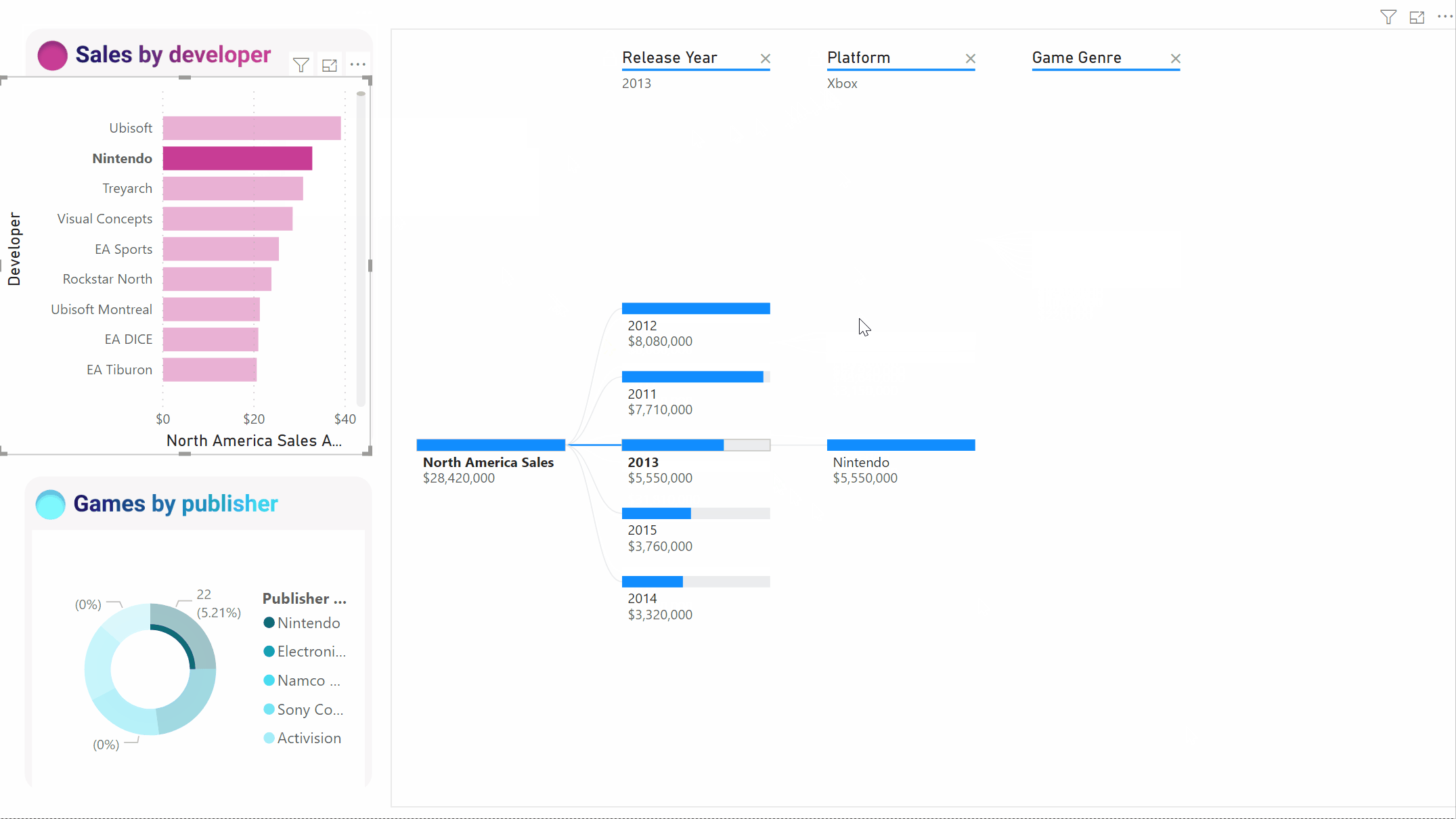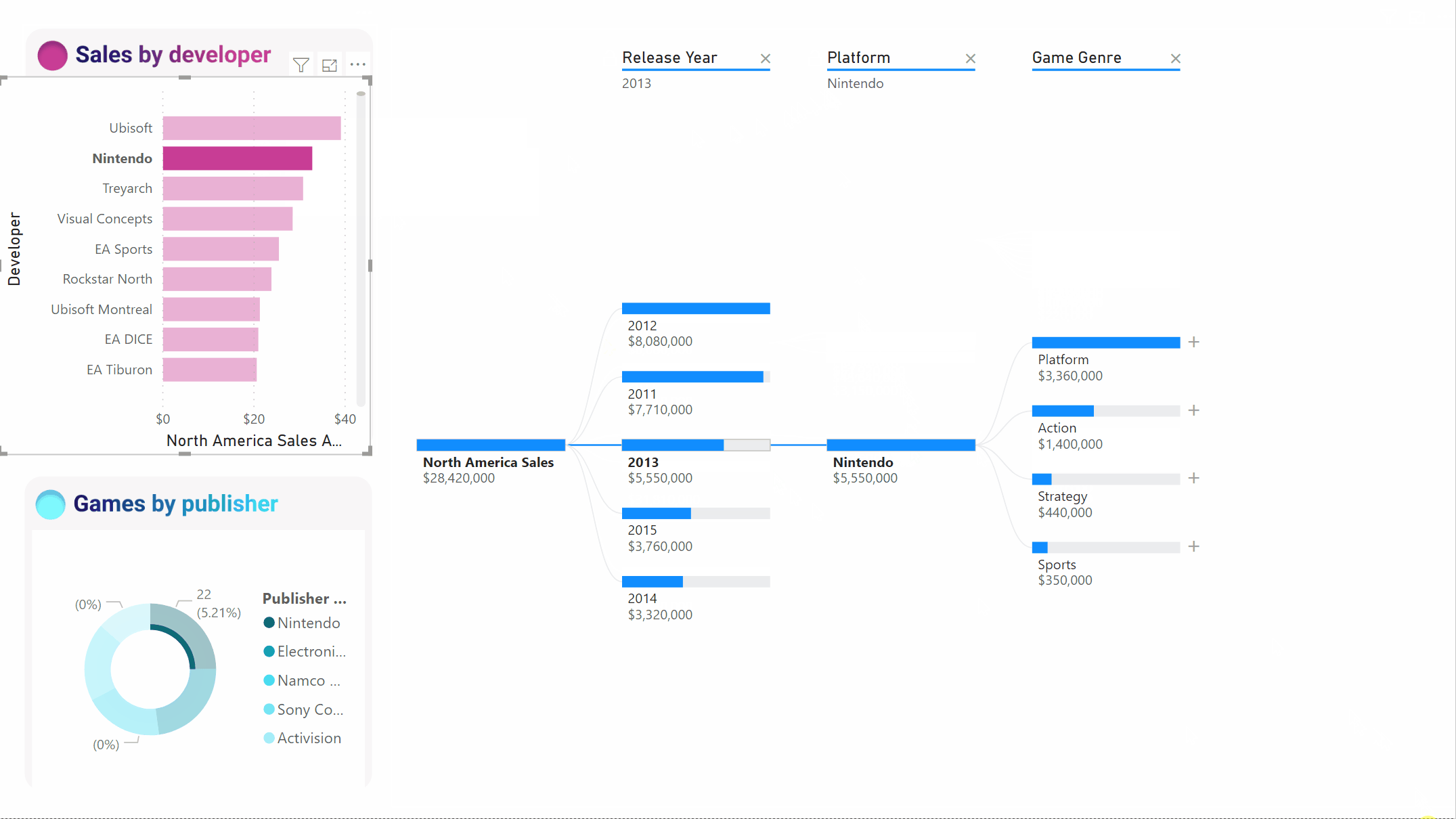
При взаимодействии с другими визуальными элементами осуществляется перекрестная фильтрация дерева декомпозиции. В результате порядок узлов в уровнях может измениться. В приведенном ниже примере выполнена перекрестная фильтрация дерева по критерию Ubisoft. Путь обновляется, и продажи Xbox перемещаются с первого на второе место, уступая первенство PlayStation.

Если затем перекрестно отфильтровать дерево по Nintendo, продажи Xbox будут пустыми, так как игры Nintendo, разработанные для Xbox, отсутствуют. Xbox, а также его последующий путь, отфильтровывается из представления.

Несмотря на то что путь не отображается, существующие уровни (в нашем случае игровой жанр) остаются закрепленными в дереве. Таким образом, при выборе узла Nintendo дерево автоматически развертывается до уровня игрового жанра.

Разбиение ИИ

Разбиение ИИ можно использовать, чтобы выяснить, где в данных следует искать дальше. Эти разбиения отображаются в верхней части списка и помечаются с помощью лампочки. Разбиение позволяет автоматически находить высокие и низкие значения в данных.

Анализ может выполняться двумя способами в зависимости от ваших предпочтений. Поведение по умолчанию выглядит следующим образом:

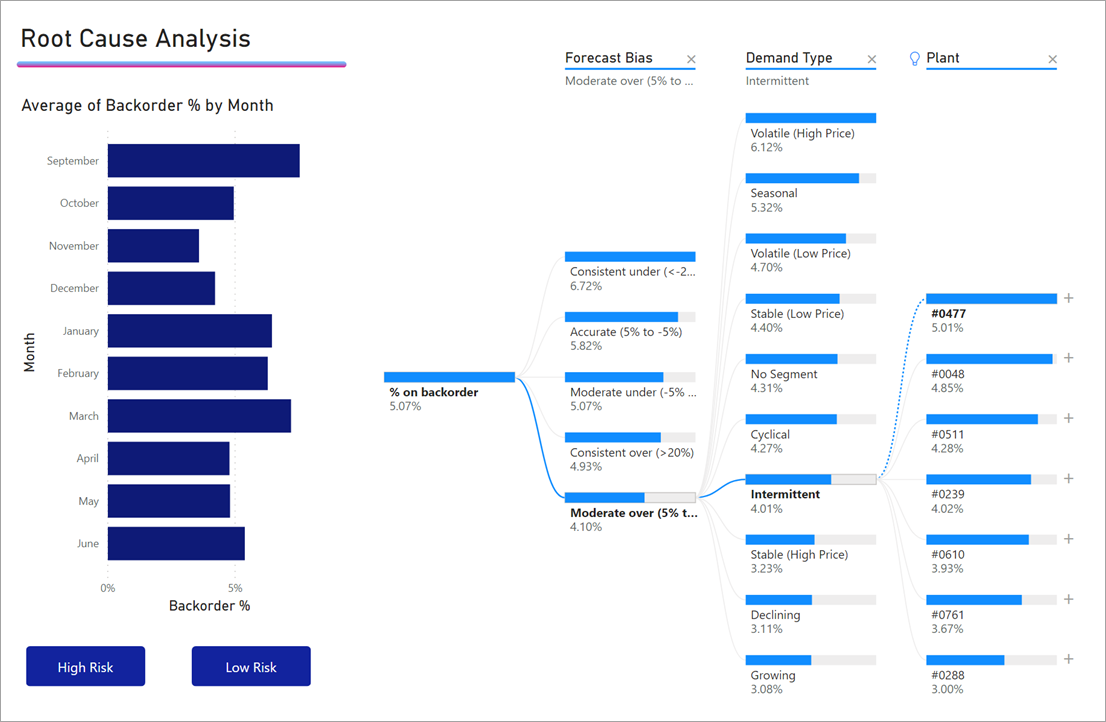
При выборе высокого значения в примере с дозаказываемым товаром выдается следующее:

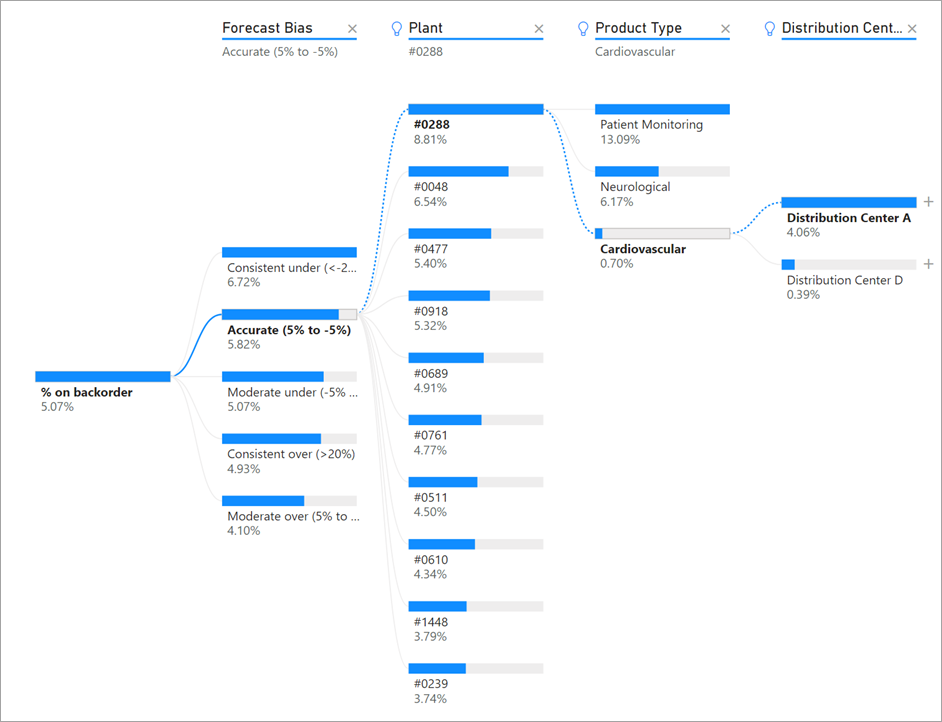
Рядом с полем Тип продукта появится лампочка, указывающая, что было выполнено разбиение ИИ. В дереве также появится пунктирная линия, рекомендующая узел Patient Monitoring (Мониторинг состояния пациентов), так как по нему определяется наибольшее значение дозаказа (9,2 %).

Наведите указатель мыши на лампочку, чтобы увидеть подсказку. В этом примере подсказка «% при дозаказе имеет наибольшее значение, если в качестве типа продукта выбран мониторинг состояния пациентов».

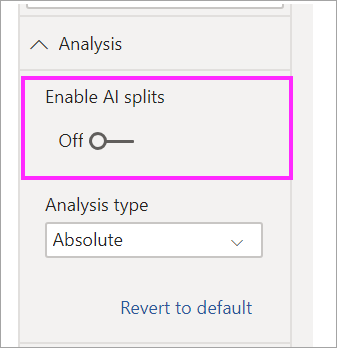
Можно настроить визуальный элемент для поиска относительных разбиений ИИ, а не абсолютных.

В относительном режиме выполняется поиск высоких значений, которые выделяются (по сравнению с остальными данными в столбце). Рассмотрим пример ниже.

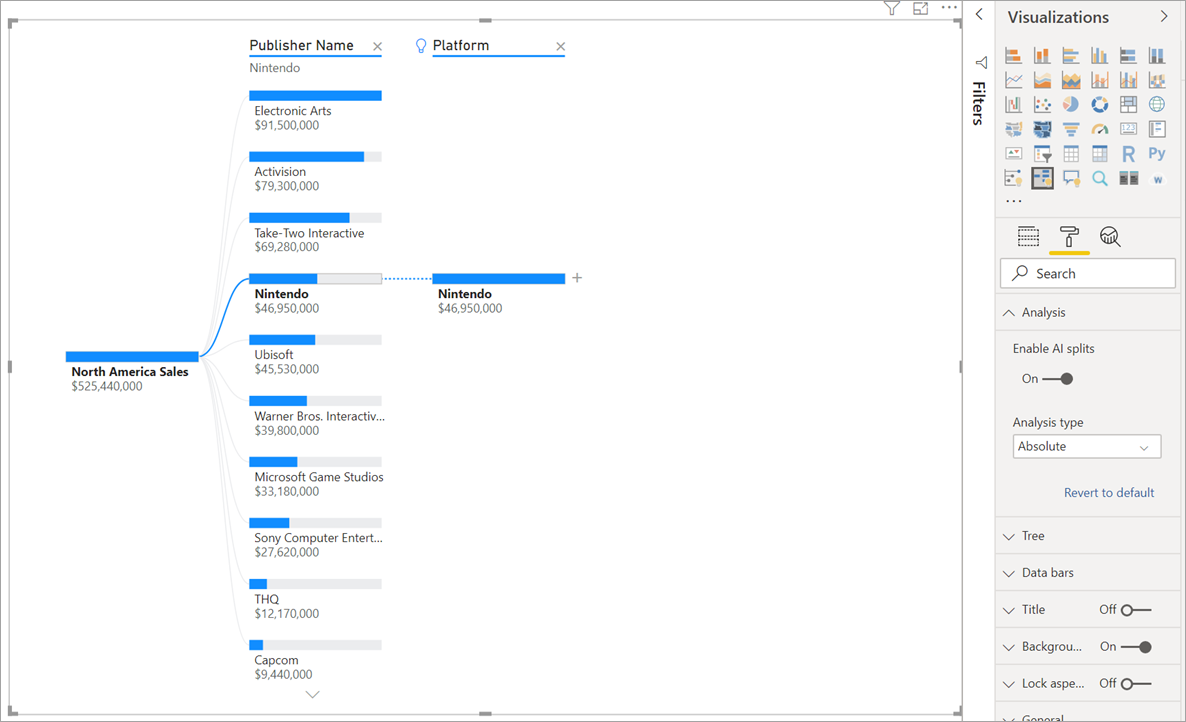
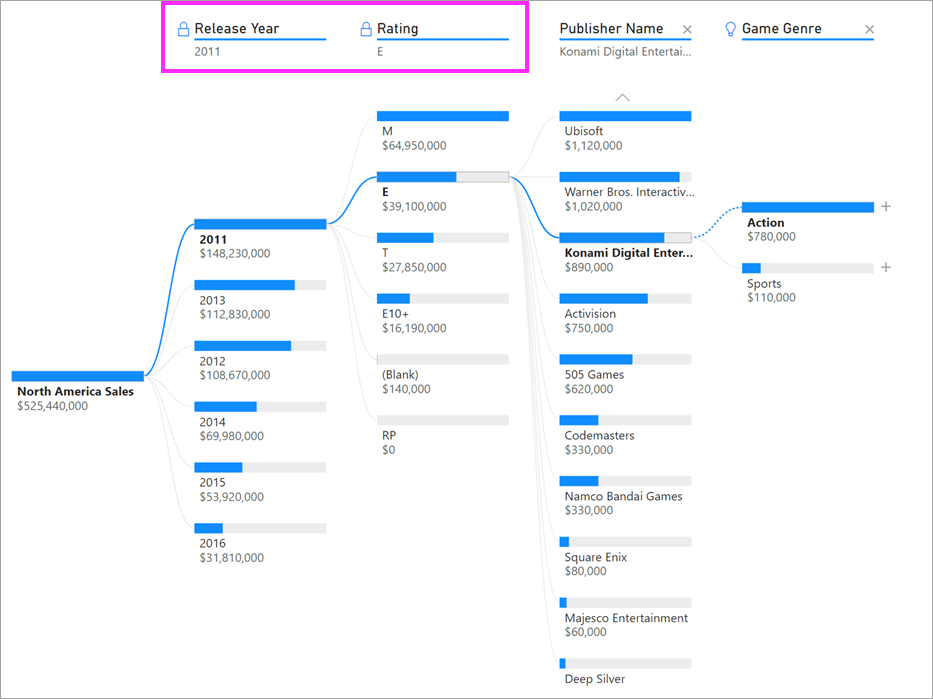
На приведенном выше снимке экрана показаны продажи видеоигр в Северной Америке. Сначала разбейте дерево по имени издателя, а затем выполните детализацию Nintendo. Если щелкнуть Высокое значение, мы получим развертывание платформы Nintendo. Так как Nintendo (издатель) разрабатывает игры только для консолей Nintendo, существует только одно значение, и поэтому неудивительно, что оно самое высокое.

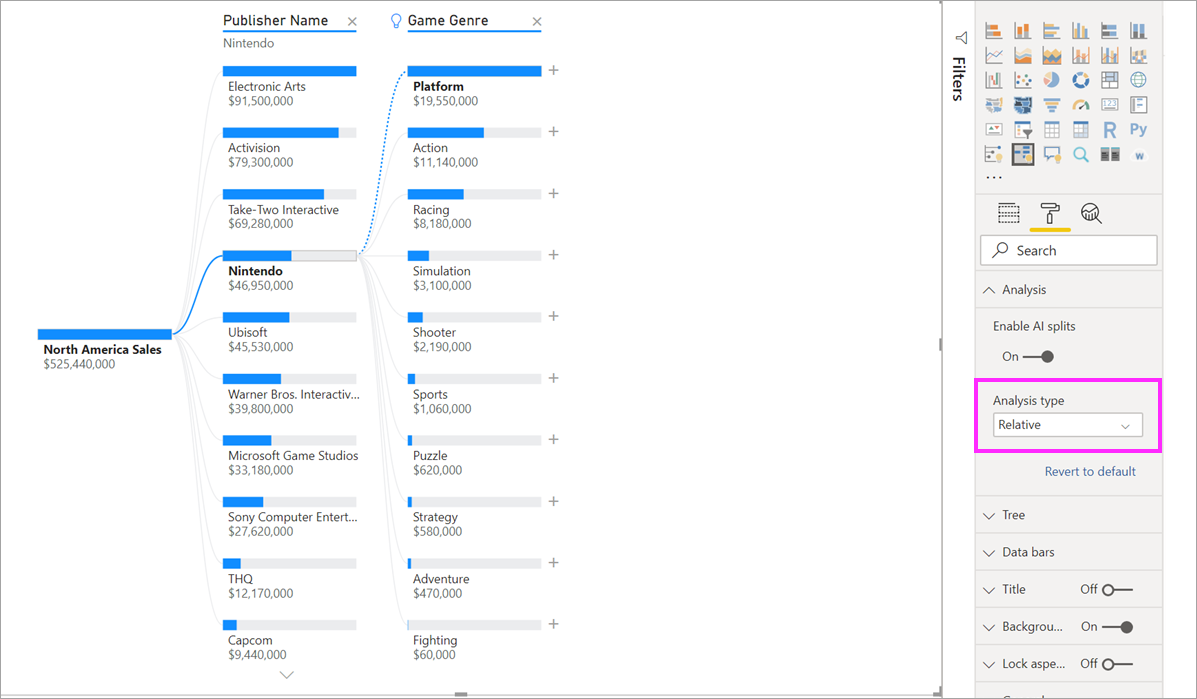
Тем не менее интереснее посмотреть, какое высокое значение выделяется относительно других значений в том же столбце. Если изменить тип анализа с абсолютного на относительный, мы получим следующий результат для Nintendo:

На этот раз рекомендуемое значение — платформа в столбце игрового жанра. Платформа не приводит к более высокому абсолютному значению, чем для Nintendo (19 950 000 по сравнению с 46 950 000 долл. США). Тем не менее это значение выделяется.

Так как в столбце игрового жанра 10 значений, ожидаемое значение для платформы — 4,6 млн долл. США, если бы они были распределены равномерно. Значение для платформы почти 20 млн долл. США. Это интересный результат, так как это в четыре раза выше ожидаемого результата.

Вычисление выполняется следующим образом.

Продажи в Северной Америке для платформ / Abs (Avg (продажи в Северной Америке для игрового жанра))
в сравнении с
продажами в Северной Америке для Nintendo / Abs (Avg (продажи в Северной Америке для платформы))

Это преобразуется в:

Если вы предпочитаете не использовать какие-либо разбиения ИИ в дереве, вы можете отключить их в разделе Analysis formatting (Форматирование анализа).

Взаимодействие элементов дерева с разбиениями ИИ

Вы можете получить несколько последующих уровней искусственного интеллекта. Вы также можете комбинировать различные виды уровней искусственного интеллекта (переход от высокого значения к низкому значению и обратно к высокому):

Если выбрать другой узел в дереве, разбиение ИИ будет пересчитано с нуля. В примере ниже мы изменили выбранный узел на уровне Forecast bias (Смещение прогноза). Последующие уровни изменяются, чтобы получить правильные высокие и низкие значения.

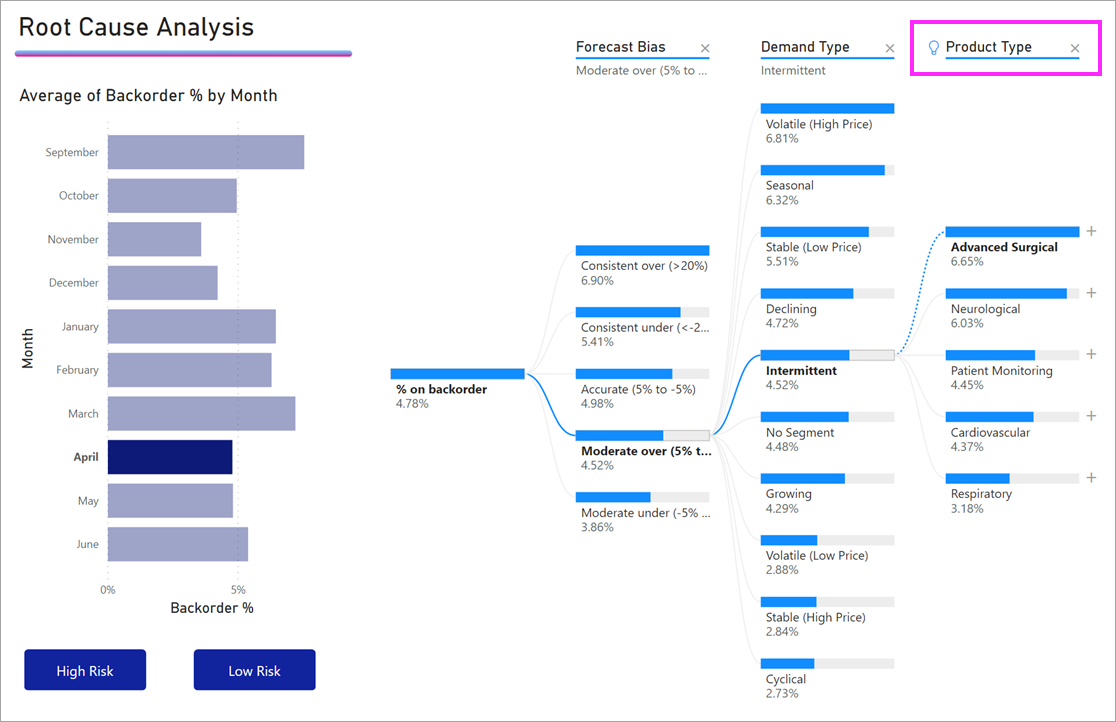
Уровни ИИ также пересчитываются при перекрестной фильтрации дерева декомпозиции по другим визуальным элементам. В приведенном ниже примере мы видим, что наш процент дозаказа является наивысшим для фабрики #0477.

Но если выбрать Апрель на линейчатой диаграмме, то наиболее высокие изменения будут для типа продукта Advanced Surgical (Перспективное хирургическое оборудование). В этом случае были переупорядочены не только узлы, но и был выбран совершенно другой столбец.

Если мы хотим, чтобы уровни с использованием ИИ вели себя как уровни без ИИ, выберите лампочку, чтобы вернуть поведение по умолчанию.

Хотя несколько уровней с ИИ можно объединить в цепочку, уровень, отличный от ИИ, не может следовать за уровнем с ИИ. Если выполнить разбиение вручную после разбиения ИИ, лампочка из уровня ИИ исчезает, а уровень преобразуется в нормальный.

Блокировка

Создатель содержимого может блокировать уровни для потребителей отчетов. Когда уровень заблокирован, его нельзя удалить или изменить. Потребитель может исследовать различные пути в пределах заблокированного уровня, но он не может изменить сам уровень. Если создатель наведет указатель на существующий уровень, отобразится значок замка. Вы можете заблокировать столько уровней, сколько хотите, но вы не сможете разблокировать уровни, предшествующие заблокированным.

В примере ниже первые два уровня заблокированы. Это означает, что пользователи отчетов могут изменять уровни 3 и 4, а затем даже добавлять новые уровни. Однако первые два уровня нельзя изменить:

Известные ограничения

Максимальное число уровней для дерева — 50. Максимальное количество точек данных, которые можно наглядно представлять в дереве, — 5000. Мы усекаем уровни, чтобы отобразить первые n уровней. В настоящее время значение первых n для каждого уровня составляет 10.

Дерево декомпозиции не поддерживается в следующих сценариях:

Разбиение ИИ не поддерживается в следующих сценариях:

Источник

Decomposition book что это

Heavy-light decompositon — это может быть просто!

Доброго времени суток всем.

Сегодня я хочу рассказать немного о написании элегантной структуру данных — Heavy-light decomposition (далее просто HLD ).

Многие из вас, наверное, сталкивались с задачами вида «дано взвешенное дерево, запросы модификации ребер и запросы нахождения минимума на ребрах между двумя вершинами». HLD умеет довольно просто решать эту и многие другие задачи.

Для начала краткое описание структуры.

// Более полное описание есть на e-maxx.

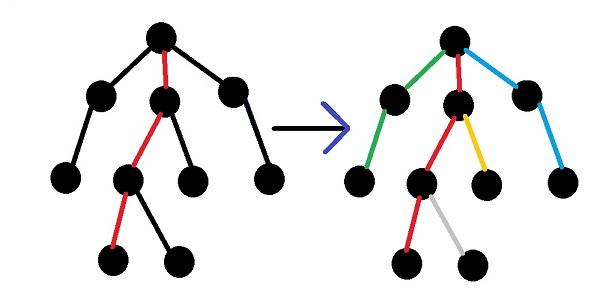
Heavy-light decomposition — это такая разбивка графа на непересекающиеся по вершинам или ребрам пути, что на пути от любой вершины до корня этого дерева мы сменим не более log(N) путей. Если мы научимся строить такие пути, то с помощью дополнительных структур (дерево отрезков (или просто ДО), например) сможем быстро отвечать на запросы.

Назовем ребро тяжелым, если поддерево сына, в которого ведет это ребро, будет по размеру не менее половины поддерева отца. Другими словами, 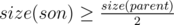. Заметим, что с вершины вниз может выходить не более одного тяжелого ребра.

«И что это нам дает?» — спросите Вы. А дает это нам следующее: если мы возьмем все вершины, из которых не выходит тяжелое ребро, и будем подниматься к корню, пока его не достигнем или не пройдем по легкому ребру, то это и будут нужные нам пути.

Построив дерево отрезков над каждым из путей, мы сможем за log 2 (N) отвечать на самые разные запросы между двумя вершинами (максимум и т.д.). Нужно будет аккуратно подниматься от вершин к их lca (наименьший общий предок) и производить запросы на ДО или на еще чём-то.

Теперь о количестве кода..

О построении HLD

И это возможно. Можно строить декомпозицию так: пускай мы находимся в некоторой вершине. Она принадлежит некоторому пути. Рассмотрим всех сынов этой вершины — мы можем продолжить этот путь только в одного, а все остальные сыны станут началом новых путей. В какого же сына надо продолжить этот путь? Правильно, в того, у которого наибольшее поддерево. Значит, один dfs нужен, чтобы подсчитать размеры поддеревьев, а другой для непосредственного построения декомпозиции.

Об отдельных структурах для каждого пути

О честном нахождении lca

Оказывается, что не нужно искать lca я явном виде. Давайте поступим по следующему алгоритму: рассмотрим два пути, на которых сейчас наши вершины. Если они на одном пути, то это просто запрос на ДО. А если нет? Тогда давайте выберем путь, у которого наивысшая вершина ниже. Далее просто перейдем в предка этой вершины. Будем так продолжать, пока не придем в один путь. Параллельно всем этим подъемам будем делать запросы на ДО, тем самым ища ответ.

Имеем, что ответ на запрос и нахождение lca можно делать одновременно.

Материалы

Я очень благодарен сайту e-maxx, на котором есть хорошее описание (клац) этой структуры. Я много в чем опирался именно на эту статью.

Еще хорошие материалы есть здесь.

И короткая реализация есть здесь

Бонус

Можно проверить свою HLD на этой задаче. А здесь мой код к ней.

Источник

Decomposition book что это

A supervised machine learning model can be viewed as a function that takes a high-dimensional feature vector as input and produces a prediction or classification score as output. Functional decomposition is an interpretation technique that deconstructs the high-dimensional function and expresses it as a sum of individual feature effects and interaction effects that can be visualized. In addition, functional decomposition is a fundamental principle underlying many interpretation techniques – it helps you better understand other interpretation methods.

Let us jump right in and look at a particular function. This function takes two features as input and produces a one-dimensional output:

\[y = \hat(x_1, x_2) = 2 + e^ — x_2 + x_1 \cdot x_2\]

Think of the function as a machine learning model. We can visualize the function with a 3D plot or a heatmap with contour lines:

\[\hat(x_1, x_2) = \hat_0 + \hat_1(x_1) + \hat_2(x_2) + \hat_<1,2>(x_<1>,x_<2>)\]

The main effects indicate how each feature affects the prediction, independent of the values the other feature. The interaction effect indicates the joint effect of the features. The intercept simply tells us what the prediction is when all feature effects are set to zero. Note that the components themselves are functions (except for the intercept) with different input dimensionality.

FIGURE 8.23: Decomposition of a function.

8.4.1 How not to Compute the Components I

To solve problem 1) of lack of access to a neat formula, we need a method that uses only the prediction function or classification score. To solve problem 2) of lack of definition, we need some axioms that tell us what the components should look like and how they relate to each other. But first, we should define more precisely what functional decomposition is.

8.4.2 Functional Decomposition

A prediction function takes \(p\) features as input, \(\hat: \mathbb^p \mapsto \mathbb\) and produces an output. This can be a regression function, but it can also be the classification probability for a given class or the score for a given cluster (unsupervised machine learning). Fully decomposed, we can represent the prediction function as the sum of functional components:

\[\begin \hatx) = & \hat_0 + \hat_1(x_1) + \ldots + \hat_p(x_p) \\ & + \hat_<1,2>(x_1, x_2) + \ldots + \hat_<1,p>(x_1, x_p) + \ldots + \hat_(x_, x_p) \\ & + \ldots \\ & + \hat_<1,\ldots,p>(x_1, \ldots, x_p) \end\]

How many components are in the above formula? The answer boils down to how many possible subsets \(S\) of the features \(1,\ldots, p\) we can form. And these are \(\sum_^p\binom

=2^p\) possible subsets! For example, if a function uses 10 features, we can decompose the function into 1042 components: 1 intercept, 10 main effects, 90 2-way interaction terms, 720 3-way interaction terms, … And with each additional feature, the number of components doubles. Clearly, for most functions, it is not feasible to compute all components. Another reasons NOT to compute all components is that components with \(|S|>2\) are difficult to visualize and interpret.

8.4.3 How not to Compute the Components II

So far I have avoided talking about how the components are defined and computed. The only constraints we have implicitly talked about were that the sum of components should yield the original function, and which components are used with which dimensionality are used. But without further constraints on what the components should be, they are not unique. This means we could shift effects between main effects and interactions, or lower order interactions (few features) and higher-order interactions (more features). In the example at beginning of the chapter we could set both main effects to zero, and add their effects to the interaction effect.

The ambiguity can be avoided by specifying further constraints or specific methods for computing the components. In this chapter, we will discuss three methods that approach the functional decomposition in different ways.

8.4.4 Functional ANOVA

Hooker (2004) defines each component with the following formula:

Okay, let us take this thing apart. We can rewrite the component as:

This example shows how each higher order effect is defined by integrating over all other features, but also by removing all the lower order effects that are subsets of the feature set we are interested in.

Hooker (2004) has shown that this definition of functional components satisfies these desirable axioms:

The zero means axiom implies that all effects or interactions are centered around zero. As a consequence, the interpretation at a position x is relative to the centered prediction and not the absolute prediction.

Variance decomposition allows us to divide the variance of the function \(f\) among the components, and guarantees that it adds up the total variance of the function in the end. The variance decomposition property can also explain to us why the method is called «functional ANOVA’’. In statistics, ANOVA stands for ANalysis Of VAriance. ANOVA refers to a collection of methods that analyze differences in the mean of a target variable. ANOVA works by dividing the variance and attributing it to the variables. Functional ANOVA can therefore be seen as an extension of this concept to any function.

Problems arise with the functional ANOVA when features are correlated. As a solution, the generalized functional ANOVA has been proposed.

8.4.5 Generalized Functional ANOVA for Dependent Features

Similar to most interpretation techniques based on sampling data (such as the PDP), the functional ANOVA can produce misleading results when features are correlated. If we integrate over the uniform distribution, when in reality feature are dependent, we create a new dataset that deviates from the joint distribution and extrapolates to unlikely combinations of feature values.

Hooker (2007) 40 proposed the generalized functional ANOVA, a decomposition that works for dependent features. It is a generalization of the functional ANOVA we encountered earlier, which means that the functional ANOVA is a special case of the generalized functional ANOVA. The components are defined as projections of f onto the space of additive functions:

Instead of orthogonality, the components satisfy a hierarchical orthogonality condition:

\[\forall \hat_S(x_S)| S \subset U: \int \hat_S(x_S) \hat_U(x_U) w(x)dx = 0\]

The estimation is done on a grid of points in the feature space and is stated as a minimization problem that can be solved using regression techniques. However, the components cannot be computed individually, nor hierarchically, but a complex system of equations involving other components has to be solved. The computation is therefore quite complex and computationally intensive.

8.4.6 Accumulated Local Effect Plots

As Apley and Zhu (2021) note, pseudo-orthogonality may be more desirable than hierarchical orthogonality, because it does not entangle marginal effects of the features. Furthermore, ALE does not require estimation of the joint distribution; the components can be estimated in a hierarchical manner, which means that calculating the 2D ALE for features 1 and 2 requires only the calculations of individual ALE components of 1 and 2 and the intercept term in addition.

8.4.7 Statistical Regression Models

This approach ties in with interpretable models, in particular generalized additive models. Instead of decomposing a complex function, we can build constraints into the modeling process so that we can easily read out the individual components. While decomposition can be handled in a top-down manner, where we start with a high-dimensional function and decompose it, generalized additive models provide a bottom-up approach, where we build the model from simple components. Both approaches have in common that their goal is to provide individual and interpretable components. In statistical models, we restrict the number of components so that not all \(2^p\) components have to be fitted. The simplest version is linear regression:

\[\hatx) = \beta_0 + \beta_1 x_1 + \ldots \beta_p x_p\]

The generalized additive model relaxes the second assumption by allowing more flexible functions \(\hat_j\) through the use of splines. Interactions can also be added, but this process is rather manual. Approaches such as GA2M attempt to add 2-way interactions automatically to a GAM. 42

Thinking of a linear regression model or a GAM as functional decomposition can also lead to confusion. If you apply the decomposition approaches from earlier in the chapter (generalized functional ANOVA and accumulated local effects), you may get components that are different from the components read directly from the GAM. This can happen when interaction effects of correlated features are modeled in the GAM. The discrepancy occurs because other functional decomposition approaches split effects differently between interactions and main effects.

So when should you use GAMs instead of a complex model + decomposition? You should stick to GAMs when most interactions are zero, especially when there are not interactions with three or more features. If we know that the maximum number of features involved in interactions is two ( \(|S|\leq<>2\) ), then we can use approaches like MARS or GA2M. Ultimately, model performance on test data may indicate whether a GAM is sufficient or a more complex model performs much better.

8.4.8 Bonus: Partial Dependence Plot

8.4.9 Advantages

I consider functional decomposition to be a core concept of machine learning interpretability.

Functional decomposition gives us a theoretical justification for decomposing high-dimensional and complex machine learning models into individual effects and interactions – a necessary step that allows us to interpret individual effects. Functional decomposition is the core idea for techniques such as statistical regression models, ALE, (generalized) functional ANOVA, PDP, the H-statistic, and ICE curves.

Functional decomposition also provides a better understanding of other methods. For example, permutation feature importance breaks the association between a feature and the target. Viewed through the functional decomposition lens, we can see that the permutation “destroys” the effect of all components in which the feature was involved. This affects the main effect of the feature, but also all interactions with other features. As another example, Shapley values decompose a prediction into additive effects of the individual feature. But the functional decomposition tells us that there should also be interaction effects in the decomposition, so where are they? Shapley values provide a fair attribution of effects to the individual features, meaning that all interactions are also fairly attributed to the features and therefore divided up among the Shapley values.

When considering functional decomposition as a tool, the use of ALE plots offers many advantages. ALE plots provide a functional decomposition that is fast to compute, has software implementations (see the ALE chapter), and desirable pseudo-orthogonality properties.

8.4.10 Disadvantages

The concept of functional decomposition quickly reaches its limits for high-dimensional components beyond interactions between two features. Not only does this exponential explosion in the number of features limit practicability, since we cannot easily visualize higher order interactions, but computational time is insane if we were to compute all interactions.

Each method of functional decomposition method has. The bottom-up approach – constructing regression models – has the disadvantage of being a quite manual process that imposes many constraints on the model that can affect predictive performance. Functional ANOVA requires independent features. Generalized functional ANOVA is very difficult to estimate. Accumulated local effect plots do not provide a variance decomposition.

The functional decomposition approach is more appropriate for analysing tabular data than text or images.

Hooker, Giles. “Discovering additive structure in black box functions.” Proceedings of the tenth ACM SIGKDD international conference on Knowledge discovery and data mining. 2004.↩︎

Hooker, Giles. “Generalized functional anova diagnostics for high-dimensional functions of dependent variables.” Journal of Computational and Graphical Statistics 16.3 (2007): 709-732.↩︎

Apley, Daniel W., and Jingyu Zhu. “Visualizing the effects of predictor variables in black box supervised learning models.” Journal of the Royal Statistical Society: Series B (Statistical Methodology) 82.4 (2020): 1059-1086.↩︎

Caruana, Rich, et al. “Intelligible models for healthcare: Predicting pneumonia risk and hospital 30-day readmission.” Proceedings of the 21th ACM SIGKDD international conference on knowledge discovery and data mining. 2015.↩︎

Источник