6 в чем заключаются многоалфавитные подстановки
Простые криптосистемы
Криптографические методы являются наиболее эффективными средствами защиты информации в автоматизированных системах (АС). А при передаче информации по протяженным линиям связи они являются единственным реальным средством предотвращения несанкционированного доступа.
Основные требования к криптографическому закрытию информации в АС
Классификация основных методов криптографического закрытия информации
Шифрование методом замены (подстановки)
Наиболее простой метод шифрования. Символы шифруемого текста заменяются другими символами, взятыми из одного алфавита (одноалфавитная замена) или нескольких алфавитов (многоалфавитная подстановка).
Одноалфавитная подстановка
Примеры таблиц замены:
Стойкость метода простой замены низкая. Зашифрованный текст имеет те же самые статистические характеристики, что и исходный, поэтому зная стандартные частоты появления символов в том языке, на котором написано сообщение, и подбирая по частотам появления символы в зашифрованном сообщении, можно восстановить таблицу замены. Для этого требуется лишь достаточно длинный зашифрованный текст, для того, чтобы получить достоверные оценки частот появления символов. Поэтому простую замену используют лишь в том случае, когда шифруемое сообщение достаточно коротко!
Многоалфавитная замена повышает стойкость шифра.
Многоалфавитная одноконтурная обыкновенная подстановка
Таблица Вижинера для русского алфавита:
При шифровании и дешифровании нет необходимости держать в памяти всю матрицу Вижинера, поскольку используя свойства циклического сдвига, можно легко вычислить любую строку матрицы по ее номеру и первой строке.
Используя свойства циклического сдвига влево элементы k-ой строки можно выразить через элементы первой строки
При дешифровании производится обратная замена
Таким образом при дешифровании по k-ой строке матрицы Вижинера символа из зашифрованного текста, значение которого равно a(1,j), проводится обратная подстановка
Многоалфавитная одноконтурная монофоническая подстановка
В монофонической подстановке количество и состав алфавитов выбирается таким образом, чтобы частоты появления всех символов в зашифрованном тексте были одинаковыми. При таком положении затрудняется криптоанализ зашифрованного текста с помощью его статистической обработки. Выравнивание частот появления символов достигается за счет того, что для часто встречающихся символов исходного текста предусматривается большее число заменяющих символов, чем для редко встречающихся.
Пример таблицы монофонической замены:
Шифрование проводится так же, как и при простой подстановке, с той лишь разницей, что после шифрования каждого символа соответствующий ему столбец алфавитов циклически сдвигается вверх на одну позицию. Таким образом, столбцы алфавитов как бы образуют независимые друг от друга кольца, поворачиваемые вверх на один знак каждый раз после шифрования соответствующего знака исходного текста.
Многоалфавитная многоконтурная подстановка
Многоконтурная подстановка заключается в том, что для шифрования используются несколько наборов (контуров) алфавитов, используемых циклически, причем каждый контур в общем случае имеет свой индивидуальный период применения. Частным случаем многоконтурной полиалфавитной подстановки является замена по таблице Вижинера, если для шифрования используется несколько ключей, каждый из которых имеет свой период применения.
Общая модель шифрования подстановкой может быть представлена в следующем виде:
Шифрование методом перестановки
При шифровании перестановкой символы шифруемого текста переставляются по определенным правилам внутри шифруемого блока этого текста.
Простая перестановка
Выбирается размер блока шифрования в n столбцов и m строк и ключевая последовательность, которая формируется из натурального ряда чисел 1,2. n случайной перестановкой.
Например, зашифруем текст
блоком размером 8*3 и ключом 5-8-1-3-7-4-6-2.
Таблица простой перестановки будет иметь вид:
Ключ 5 8 1 3 7 4 6 2
Г Р У З И Т Е _ А П Е Л Ь С И Н Ы _ Б О Ч К А Х
Перестановка, усложненная по таблице
При усложнении перестановки по таблицам для повышения стойкости шифра в таблицу перестановки вводятся неиспользуемые клетки таблицы. Количество и расположение неиспользуемых элементов является дополнительным ключом шифрования.
Для дальнейшего увеличения криптостойкости шифра можно в процессе шифрования менять ключи, размеры таблицы перестановки, количество и расположение неиспользуемых элементов по некоторому алгоритму, причем этот алгоритм становится дополнительным ключом шифра.
Перестановка, усложненная по маршрутам
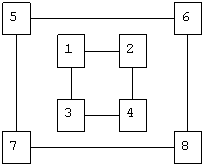
Высокую стойкость шифрования можно обеспечить усложнением перестановок по маршрутам типа гамильтоновских. При этом для записи символов шифруемого текста используются вершины некоторого гиперкуба, а знаки зашифрованного текста считываются по маршрутам Гамильтона, причем используются несколько различных маршрутов. Для примера рассмотрим шифрование по маршрутам Гамильтона при n=3.
Струкрура трехмерного гиперкуба:
Номера вершин куба определяют последовательность его заполнения символами шифруемого текста при формировании блока. В общем случае n-мерный гиперкуб имеет n 2 вершин.
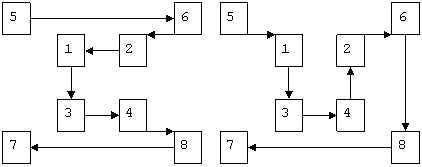
Маршруты Гамильтона имеют вид:
Последовательность перестановок символов в шифруемом блоке для первой схемы 5-6-2-1-3-4-8-7, а для второй 5-1-3-4-2-6-8-7. Аналогично можно получить последовательность перестановок для других маршрутов: 5-7-3-1-2-6-8-4, 5-6-8-7-3-1-2-4, 5-1-2-4-3-7-8-6 и т.д.
Размерность гиперкуба, количество вид выбираемых маршрутов Гамильтона составляют секретный ключ метода.
Стойкость простой перестановки однозначно определяется размерами используемой матрицы перестановки. Например, при использовании матрицы 16*16 число возможных перестановок достигает 1.4E26. Такое число вариантов невозможно перебрать даже с использованием ЭВМ. Стойкость усложненных перестановок еще выше. Однако следует иметь в виду, что при шифровании перестановкой полностью сохраняются вероятностные характеристики исходного текста, что облегчает криптоанализ.
Шифрование методом гаммирования
Суть метода состоит в том, что символы шифруемого текста последовательно складываются с символами некоторой специальной последовательности, называемой гаммой. Иногда такой метод представляют как наложение гаммы на исходный текст, поэтому он получил название «гаммирование«.
Наложение гаммы можно осуществить несколькими способами, например по формуле
Расшифрование текста проводится по той же формуле:
Последовательность гаммы удобно формировать с помощью датчика псевдослучайных чисел (ПСЧ).
Стойкость гаммирования однозначно определяется длиной периода гаммы. При использовании современных ПСЧ реальным становится использование бесконечной гаммы, что приводит к бесконечной теоретической стойкости зашифрованного текста.
Шифрование с помощью аналитических преобразований
В качестве ключа задается квадратная матрица ||a|| размера n*n. Исходный текст разбивается на блоки длиной n символов. Каждый блок рассматривается как n-мерный вектор. А процесс шифрования блока заключается в получении нового n-мерного вектора (зашифрованного блока) как результата умножения матрицы ||a|| на исходный вектор.
Расшифрование текста происходит с помощью такого же преобразования, только с помощью матрицы, обратной ||a||. Очевидно, что ключевая матрица ||a|| должна быть невырожденной.
Комбинированные методы шифрования
Достаточно эффективным средством повышения стойкости шифрования является комбинированное использование нескольких различных способов шифрования, т.е. последовательное шифрование исходного текста с помощью двух или более методов.
Стойкость комбинированного шифрования S не ниже произведения стойкостей используемых способов
Если какой-либо способ шифрования при независимом применении может обеспечить стойкость не ниже S, то комбинировать его с другими способами целесообразно лишь при выполнении условия
Организационные проблемы криптозащиты
Рассмотренные значения стойкости шифров являются потенциальными величинами. Они могут быть реализованы при строгом соблюдении правил использования криптографических средств защиты.
Под дублированием здесь понимается повторное шифрование одного и того же отрывка текста с использованием тех же ключей (например, если при первом шифровании произошел сбой). Нарушение этого правила резко снижает надежность шифрования, так как исходный текст может быть восстановлен с помощью статистического анализа двух вариантов зашифрованного текста.
Нельзя допускать злоумышленнику возможности направить в систему ряд специально подобранных сообщений и получать их в зашифрованном виде. Такого взлома не может выдержать ни одна криптосистема!
Важными аспектами организации криптозащиты являются выбор способа закрытия, распределение ключей и доставка их в места пользования (механизм распределения ключей).
Выбор способа защиты тесно связан с трудоемкостью метода шифрования, степенью секретности закрываемых данных, стойкостью метода и объемом шифруемой информации.
Простейшие методы шифрования с закрытым ключом
Пропорциональные шифры
К одноалфавитным методам подстановки относятся пропорциональные или монофонические шифры, в которых уравнивается частота появления зашифрованных знаков для защиты от раскрытия с помощью частотного анализа. Для знаков, встречающихся часто, используется относительно большое число возможных эквивалентов. Для менее используемых исходных знаков может оказаться достаточным одного или двух эквивалентов. При шифровании замена для символа открытого текста выбирается либо случайным, либо определенным образом (например, по порядку).
При использовании пропорционального шифра в качестве замены символам обычно выбираются числа. Например, поставим в соответствие буквам русского языка трехзначные числа, как указано на таблица 2.5.
| Символ | Варианты замены | Символ | Варианты замены | ||||||||
| А | 760 | 128 | 350 | 201 | С | 800 | 767 | 105 | |||
| Б | 101 | Т | 759 | 135 | 214 | ||||||
| В | 210 | 106 | У | 544 | |||||||
| Г | 351 | Ф | 560 | ||||||||
| Д | 129 | Х | 768 | ||||||||
| Е | 761 | 130 | 802 | 352 | Ц | 545 | |||||
| Ж | 102 | Ч | 215 | ||||||||
| З | 753 | Ш | 103 | ||||||||
| И | 762 | 211 | 131 | Щ | 752 | ||||||
| К | 754 | 764 | Ъ | 561 | |||||||
| Л | 132 | 354 | Ы | 136 | |||||||
| М | 755 | 742 | Ь | 562 | |||||||
| Н | 763 | 756 | 212 | Э | 750 | ||||||
| О | 757 | 213 | 765 | 133 | 353 | Ю | 570 | ||||
| П | 743 | 766 | Я | 216 | 104 | ||||||
| Р | 134 | 532 | Пробел | 751 | 769 | 758 | 801 | 849 | 035… | ||
В этом случае сообщение
может быть зашифровано следующим образом:
В данном примере варианты замен для повторяющихся букв (например, «О» ) выбирались по порядку.
Интересно, что шифры, в которых производится замена букв несколькими символами, пропорционально встречаемости в открытом тексте, описывали итальянские ученые еще в XIV-XV веках.
Пропорциональные шифры более сложны для вскрытия, чем шифры простой одноалфавитной замены. Однако, если имеется хотя бы одна пара «открытый текст – шифротекст», вскрытие производится тривиально. Если же в наличии имеются только шифротексты, то вскрытие ключа, то есть нахождение таблицы замен, становится более трудоемким, но тоже вполне осуществимым.
Многоалфавитные подстановки
В целях маскирования естественной частотной статистики исходного языка применяется многоалфавитная подстановка, которая также бывает нескольких видов. В многоалфавитных подстановках для замены символов исходного текста используется не один, а несколько алфавитов. Обычно алфавиты для замены образованы из символов исходного алфавита, записанных в другом порядке.
Примером многоалфавитной подстановки может служить схема, основанная на использовании таблицы Вижинера. Этот метод, известный уже в XVI веке, был описан французом Блезом Вижинером в «Трактате о шифрах», вышедшем в 1585 году.
| АБВГДЕ. | . ЭЮЯ |
| БВГДЕЖ. | . ЮЯА |
| ВГДЕЖЗ. | . ЯАБ |
| ГДЕЖЗИ. | . АБВ |
| ДЕЖЭИК. | . БВГ |
| ЕЖЗИКЛ. | . ВГД |
| . | . |
| ЯАБВГД. | . ЬЭЮ |
Для шифрования текста выбирают ключ, представляющий собой некоторое слово или набор символов исходного алфавита. Далее из полной матрицы выписывают подматрицу шифрования, включающую первую строку и строки матрицы, начальными буквами которых являются последовательно буквы ключа (например, если выбрать ключ «весна», то таблица шифрования будет такой, как на таблица 2.7).
| АБВГДЕЖЗИКЛМНОПРСТУФХЦЧШЩЪЫЬЭЮЯ |
| ВГДЕЖЗИКЛМНОПРСТУФХЦЧШЩЪЫЬЭЮЯАБ |
| ЕЖЗИКЛМНОПРСТУФХЦЧШЩЪЫЬЭЮЯАБВГД |
| НОПРСТУФХЦЧШЩЪЫЬЭЮЯАБВГДЕЖЗИКЛМ |
| СТУФХЦЧШЩЪЫЬЭЮЯАБВГДЕЖЗИКЛМНОПР |
В процессе шифрования ( рис. 2.5) под каждой буквой шифруемого текста записывают буквы ключа, повторяющие ключ требуемое число раз, затем шифруемый текст по таблице шифрования ( таблица 2.7) заменяют буквами, расположенными на пересечениях линий, соединяющих буквы текста первой строки таблицы и буквы ключа, находящейся под ней.
Рассмотрим на примере процесс расшифрования сообщения по методу Вижинера. Пусть имеется зашифрованное с помощью ключа ВЕСНА сообщение КЕКХТВОЭЦОТССВИЛ (пробелы при шифровании пропущены). Расшифровка текста выполняется в следующей последовательности ( таблица 2.8):
| КЛЮЧ | ВЕСНАВЕСНАВЕСНАВ |
| ЗАШИФРОВАННЫЙ ТЕКСТ | КЕКХТВОЭЦОТССВИЛ |
| РАСШИФРОВАННЫЙ ТЕКСТ | ЗАЩИТАИНФОРМАЦИИ |
| ИСХОДНЫЙ ТЕКСТ | ЗАЩИТА ИНФОРМАЦИИ |
Раскрыть шифр Вижинера, тем же способом, что и шифр одноалфавитной замены, невозможно, так как одни и те же символы открытого текста могут быть заменены различными символами зашифрованного текста. С другой стороны, различные буквы открытого текста могут быть заменены одинаковыми знаками зашифрованного текста.
Особенность данного метода многоалфавитной подстановки заключается в том, что каждый из символов ключа используется для шифрования одного символа исходного сообщения. После использования всех символов ключа, они повторяются в том же порядке. Если используется ключ из десяти букв, то каждая десятая буква сообщения шифруется одним и тем же символом ключа. Этот параметр называется периодом шифра. Если ключ шифрования состоит из одного символа, то при шифровании будет использоваться одна строка таблицы Вижинера, следовательно, в этом случае мы получим моноалфавитную подстановку, а именно шифр Цезаря.
С целью повышения надежности шифрования текста можно использовать подряд два или более зашифрования по методу Вижинера с разными ключами (составной шифр Вижинера).
На практике кроме метода Вижинера использовались также различные модификации этого метода. Например, шифр Вижинера с перемешанным один раз алфавитом. В этом случае для расшифрования сообщения получателю необходимо кроме ключа знать порядок следования символов в таблице шифрования.
Еще одним примером метода многоалфавитной подстановки является шифр с бегущим ключом или книжный шифр. В этом методе один текст используется в качестве ключа для шифрования другого текста. В эпоху «докомпьютерной» криптографии в качестве ключа для шифра с бегущим ключом выбирали какую-нибудь достаточно толстую книгу; от этого и произошло второе название этого шифра. Периодом в таком методе шифрования будет длина выбранного в качестве ключа произведения.
Методы многоалфавитной подстановки, в том числе и метод Вижинера, значительно труднее поддаются «ручному» криптоанализу. Для вскрытия методов многоалфавитной замены разработаны специальные, достаточно сложные алгоритмы. С использованием компьютера вскрытие метода многоалфавитной подстановки возможно достаточно быстро благодаря высокой скорости проводимых операций и расчетов.
В первой половине ХХ века для автоматизации процесса выполнения многоалфавитных подстановок стали широко применять роторные шифровальные машины. Главными элементами в таких устройствах являлись роторы – механические колеса, используемые для выполнения подстановки. Роторная шифровальная машина содержала обычно клавиатуру и набор роторов. Каждый ротор содержал набор символов (по количеству в алфавите), размещенных в произвольном порядке, и выполнял простую одноалфавитную подстановку. После выполнения первой замены символы сообщения обрабатывались вторым ротором и так далее. Роторы могли смещаться, что и задавало ключ шифрования. Некоторые роторные машины выполняли также и перестановку символов в процессе шифрования. Самым известным устройством подобного класса являлась немецкая шифровальная роторная машина Энигма (лат. Enigma — загадка), использовавшаяся во время второй мировой войны. Выпускалось несколько моделей Энигмы с разным числом роторов. В шифрмашине Энигма с тремя роторами можно было использовать 16900 разных алфавитов, и все они представляли собой различные перестановки символов.
Простейшие методы шифрования с закрытым ключом
Пропорциональные шифры
К одноалфавитным методам подстановки относятся пропорциональные или монофонические шифры, в которых уравнивается частота появления зашифрованных знаков для защиты от раскрытия с помощью частотного анализа. Для знаков, встречающихся часто, используется относительно большое число возможных эквивалентов. Для менее используемых исходных знаков может оказаться достаточным одного или двух эквивалентов. При шифровании замена для символа открытого текста выбирается либо случайным, либо определенным образом (например, по порядку).
При использовании пропорционального шифра в качестве замены символам обычно выбираются числа. Например, поставим в соответствие буквам русского языка трехзначные числа, как указано на таблица 2.5.
| Символ | Варианты замены | Символ | Варианты замены | ||||||||
| А | 760 | 128 | 350 | 201 | С | 800 | 767 | 105 | |||
| Б | 101 | Т | 759 | 135 | 214 | ||||||
| В | 210 | 106 | У | 544 | |||||||
| Г | 351 | Ф | 560 | ||||||||
| Д | 129 | Х | 768 | ||||||||
| Е | 761 | 130 | 802 | 352 | Ц | 545 | |||||
| Ж | 102 | Ч | 215 | ||||||||
| З | 753 | Ш | 103 | ||||||||
| И | 762 | 211 | 131 | Щ | 752 | ||||||
| К | 754 | 764 | Ъ | 561 | |||||||
| Л | 132 | 354 | Ы | 136 | |||||||
| М | 755 | 742 | Ь | 562 | |||||||
| Н | 763 | 756 | 212 | Э | 750 | ||||||
| О | 757 | 213 | 765 | 133 | 353 | Ю | 570 | ||||
| П | 743 | 766 | Я | 216 | 104 | ||||||
| Р | 134 | 532 | Пробел | 751 | 769 | 758 | 801 | 849 | 035… | ||
В этом случае сообщение
может быть зашифровано следующим образом:
В данном примере варианты замен для повторяющихся букв (например, «О» ) выбирались по порядку.
Интересно, что шифры, в которых производится замена букв несколькими символами, пропорционально встречаемости в открытом тексте, описывали итальянские ученые еще в XIV-XV веках.
Пропорциональные шифры более сложны для вскрытия, чем шифры простой одноалфавитной замены. Однако, если имеется хотя бы одна пара «открытый текст – шифротекст», вскрытие производится тривиально. Если же в наличии имеются только шифротексты, то вскрытие ключа, то есть нахождение таблицы замен, становится более трудоемким, но тоже вполне осуществимым.
Многоалфавитные подстановки
В целях маскирования естественной частотной статистики исходного языка применяется многоалфавитная подстановка, которая также бывает нескольких видов. В многоалфавитных подстановках для замены символов исходного текста используется не один, а несколько алфавитов. Обычно алфавиты для замены образованы из символов исходного алфавита, записанных в другом порядке.
Примером многоалфавитной подстановки может служить схема, основанная на использовании таблицы Вижинера. Этот метод, известный уже в XVI веке, был описан французом Блезом Вижинером в «Трактате о шифрах», вышедшем в 1585 году.
| АБВГДЕ. | . ЭЮЯ |
| БВГДЕЖ. | . ЮЯА |
| ВГДЕЖЗ. | . ЯАБ |
| ГДЕЖЗИ. | . АБВ |
| ДЕЖЭИК. | . БВГ |
| ЕЖЗИКЛ. | . ВГД |
| . | . |
| ЯАБВГД. | . ЬЭЮ |
Для шифрования текста выбирают ключ, представляющий собой некоторое слово или набор символов исходного алфавита. Далее из полной матрицы выписывают подматрицу шифрования, включающую первую строку и строки матрицы, начальными буквами которых являются последовательно буквы ключа (например, если выбрать ключ «весна», то таблица шифрования будет такой, как на таблица 2.7).
| АБВГДЕЖЗИКЛМНОПРСТУФХЦЧШЩЪЫЬЭЮЯ |
| ВГДЕЖЗИКЛМНОПРСТУФХЦЧШЩЪЫЬЭЮЯАБ |
| ЕЖЗИКЛМНОПРСТУФХЦЧШЩЪЫЬЭЮЯАБВГД |
| НОПРСТУФХЦЧШЩЪЫЬЭЮЯАБВГДЕЖЗИКЛМ |
| СТУФХЦЧШЩЪЫЬЭЮЯАБВГДЕЖЗИКЛМНОПР |
В процессе шифрования ( рис. 2.5) под каждой буквой шифруемого текста записывают буквы ключа, повторяющие ключ требуемое число раз, затем шифруемый текст по таблице шифрования ( таблица 2.7) заменяют буквами, расположенными на пересечениях линий, соединяющих буквы текста первой строки таблицы и буквы ключа, находящейся под ней.
Рассмотрим на примере процесс расшифрования сообщения по методу Вижинера. Пусть имеется зашифрованное с помощью ключа ВЕСНА сообщение КЕКХТВОЭЦОТССВИЛ (пробелы при шифровании пропущены). Расшифровка текста выполняется в следующей последовательности ( таблица 2.8):
| КЛЮЧ | ВЕСНАВЕСНАВЕСНАВ |
| ЗАШИФРОВАННЫЙ ТЕКСТ | КЕКХТВОЭЦОТССВИЛ |
| РАСШИФРОВАННЫЙ ТЕКСТ | ЗАЩИТАИНФОРМАЦИИ |
| ИСХОДНЫЙ ТЕКСТ | ЗАЩИТА ИНФОРМАЦИИ |
Раскрыть шифр Вижинера, тем же способом, что и шифр одноалфавитной замены, невозможно, так как одни и те же символы открытого текста могут быть заменены различными символами зашифрованного текста. С другой стороны, различные буквы открытого текста могут быть заменены одинаковыми знаками зашифрованного текста.
Особенность данного метода многоалфавитной подстановки заключается в том, что каждый из символов ключа используется для шифрования одного символа исходного сообщения. После использования всех символов ключа, они повторяются в том же порядке. Если используется ключ из десяти букв, то каждая десятая буква сообщения шифруется одним и тем же символом ключа. Этот параметр называется периодом шифра. Если ключ шифрования состоит из одного символа, то при шифровании будет использоваться одна строка таблицы Вижинера, следовательно, в этом случае мы получим моноалфавитную подстановку, а именно шифр Цезаря.
С целью повышения надежности шифрования текста можно использовать подряд два или более зашифрования по методу Вижинера с разными ключами (составной шифр Вижинера).
На практике кроме метода Вижинера использовались также различные модификации этого метода. Например, шифр Вижинера с перемешанным один раз алфавитом. В этом случае для расшифрования сообщения получателю необходимо кроме ключа знать порядок следования символов в таблице шифрования.
Еще одним примером метода многоалфавитной подстановки является шифр с бегущим ключом или книжный шифр. В этом методе один текст используется в качестве ключа для шифрования другого текста. В эпоху «докомпьютерной» криптографии в качестве ключа для шифра с бегущим ключом выбирали какую-нибудь достаточно толстую книгу; от этого и произошло второе название этого шифра. Периодом в таком методе шифрования будет длина выбранного в качестве ключа произведения.
Методы многоалфавитной подстановки, в том числе и метод Вижинера, значительно труднее поддаются «ручному» криптоанализу. Для вскрытия методов многоалфавитной замены разработаны специальные, достаточно сложные алгоритмы. С использованием компьютера вскрытие метода многоалфавитной подстановки возможно достаточно быстро благодаря высокой скорости проводимых операций и расчетов.
В первой половине ХХ века для автоматизации процесса выполнения многоалфавитных подстановок стали широко применять роторные шифровальные машины. Главными элементами в таких устройствах являлись роторы – механические колеса, используемые для выполнения подстановки. Роторная шифровальная машина содержала обычно клавиатуру и набор роторов. Каждый ротор содержал набор символов (по количеству в алфавите), размещенных в произвольном порядке, и выполнял простую одноалфавитную подстановку. После выполнения первой замены символы сообщения обрабатывались вторым ротором и так далее. Роторы могли смещаться, что и задавало ключ шифрования. Некоторые роторные машины выполняли также и перестановку символов в процессе шифрования. Самым известным устройством подобного класса являлась немецкая шифровальная роторная машина Энигма (лат. Enigma — загадка), использовавшаяся во время второй мировой войны. Выпускалось несколько моделей Энигмы с разным числом роторов. В шифрмашине Энигма с тремя роторами можно было использовать 16900 разных алфавитов, и все они представляли собой различные перестановки символов.