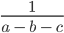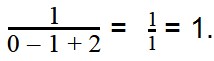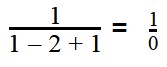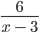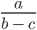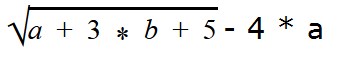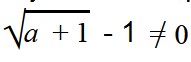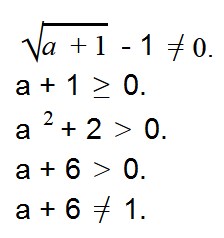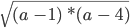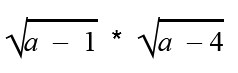2к17 что значит это выражение
2к17 что значит это выражение
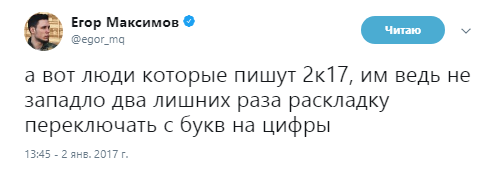
2К17 – распространенное в интернете написание года, где цифру ноль заменяют буквой К от латинского “кило” – тысяча. Тренд позаимствован из названия компьютерных игр разработчика 2K Sports.
Происхождение
У американской компании 2K Games есть подразделение 2K Sports, которое выпускает компьютерные игры о популярных в США видов спорта: бейсболе, баскетболе, хоккее. В названиях игр компания указывает год выпуска в формате 2K5 (2005) или 2K13 (2013). Например, NBA 2K12 или NHL 2K9.
Благодаря 2K Sports такое обозначение года стало популярно в геймерской среде, но уже в 2014 стало выходить за ее пределы, использоваться в соцсетях и даже названии реальных соревнований.
С каждым годом написание через К только набирало обороты. Например, в 2016 году блогер Данила Поперечный в заставке видео, посвященного нелепости слепого следования моде, написал К поверх ноля.
В 2017 году тренд достиг апогея и широко употребимым. 2К17 стали не только писать, но и произносить в устной речи. Отчасти мода на такое написание могла распространиться и благодаря популярному в России мессенджеру Telegram, в котором так сокращаются тысячи в количестве подписчиков канала (подпишитесь на Memepedia заодно).
Значение
С латыни “kilo” переводится как “тысяча”, а в обозначении года 2К17 K заменяет ноль. Вместо “две тысячи семнадцать” получается “два кило семнадцать”. Особой смысловой нагрузки замена не несет, это просто дань моде. Употребление К вместо нуля часто критикуют: это действие не облегчает и не сокращает написание года.
Слово “кило” заменяет тысячу в русском сленге довольно давно, часто так говорят о деньгах, например, “два кило баксов”.
Написание года через К ошибочное сразу с нескольких точек зрения. В Международной системе (СИ) приставку К используют для сокращения количества нулей при записи в основных единицах измерения: метр (длина), килограмм (масса), секунда (время), ампер (электрический ток), кельвин (температура), моль (количество вещества) и кандела (сила света).
Например, пишут 5К вместо 5000. Но с научной точки зрения этот принцип не используется для обычных чисел, а только для единиц измерения.
Кроме того, приставка К применима только к идущему впереди значению, то есть 2К17 это 200017. Отсутствие знака между между знаком и числом в математике означает умножение, тогда 2К*17=2000*17=34000.
В маркировке сопротивления резисторов 8K2 обозначает 8,2 килоома, то есть К стоит на месте запятой в десятичной дроби. В таком случае 2К17 это 2,17 килоома или 2170 ома. Правильным написанием 2017 через К будет 2,017К.
Галерея
А помните мы думали, что 2к17 будет лучше, чем 2к16
хахахахаха pic.twitter.com/EPS895Mtx8
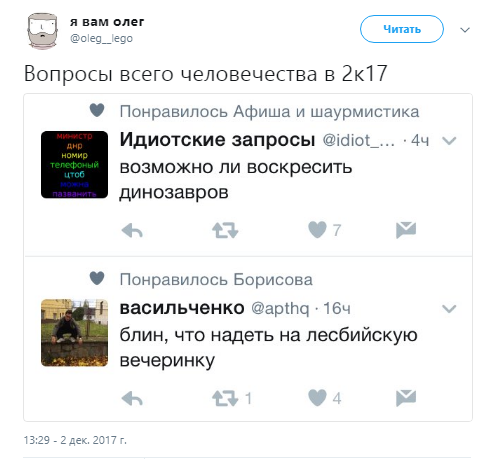
Уже заканчивается 2к17 но я все еще считаю что это лучшее что могла создать Вселенная pic.twitter.com/RUwJB9VPfT
Если вы нашли ошибку, пожалуйста, выделите фрагмент текста и нажмите Ctrl+Enter.
Ангельская нумерология 17-17
Увидев на часах дубль, остановитесь на минутку. Это высший покровитель привлекает внимание. В ангельской нумерологии комбинация 17-17 трактуется положительно. Видящий ее на верном пути. Данному сочетанию покровительствует Имамия. Ангел поможет отыскать покровителя и наставника. Запутавшегося выведет из хитрой ловушки, подстроенной недругами.
Тайны нумерологии ангелов расшифровала Дорин Верче — американский писатель и психолог. Она составила перечень самых точных толкований.
Нумерологический разбор
Каждая из цифр связана с определенной энергией. Потоки способны комбинироваться, порождая новые смыслы.
Дубль, состоящий их единицы и семерки, расшифровывается так:
Сумма 1+7+1+7=16. Принято доводит до однозначности. 1+6=7. То есть в изучаемой комбинации целых три семерки. Фактор крайне значимый.
Сам Господь вышел на связь через тандем семнадцати. Вы на пороге значительных изменений. Не страшитесь невзгод и преград. Свыше вплотную занялись вашим продвижением к счастью.
Что значит сочетание 17-17 на часах, номерах, чеках
Двойная семнадцать знаменует призыв к началу перемен в жизни, необходимости расти и развиваться во всех сферах. Покровительствует темам, непосредственно связанным с творчеством и самовыражением личности. Намекает, что впереди расцвет. Активность ныне положительно скажется на текущем благосостоянии, здоровье, психическом самоощущении. Предстоят победы и свершения.
Чем чащу видите удвоенную 17, тем жестче ангельское требование. Если мелькает постоянно, то надо поторопиться с изменениями. Иначе упустите отличный момент. Видели несколько раз — задумайтесь об усовершенствовании личностного пространства.
Дубль семнадцати несет удачу. Является прямым положительным посланием Фортуны. Вне зависимости от того, где была найденная данная комбинация чисел — на циферблате часов, кассовом чеке или номере, она говорит о приобретении высоких жизненных ценностей, новых ориентиров и надежд на светлое будущее.
Этот набор цифр исходит напрямую от божественных ангелов. Небесные жители, посылая данный знак судьбы, берут вас под своё покровительство и защиту. Просят проявлять таланты и умения, направить силы на созидание собственного благоденствия. Предлагают настойчивее трудиться, непримиримо шествовать прямиком к цели. Умоляют сохранять бодрость духа и огонь в глазах, способный заразить желанием свершений окружающих. Подобный план позволит обрести независимость и возвыситься.
Что означает в любви и отношениях
Романтическая составляющая подсказки значима для многих. Автор книги предоставил следующие объяснения по категориям:
Рожденный в семнадцать часов 17 минут обретает пожизненную удачу, успех во всех начинаниях.
Основным предзнаменованием семнадцати в нумерологии является счастье скорых и необратимых перемен.
Значимость в деньгах и работе
Символизм в материальной сфере:
Представленная комбинация цифр благоприятствует открытию собственного дела, если таковое планировалось. Подталкивает к крупному вложению капитала, к созданию прибыльного проекта.
Предназначение в творчестве
Обозначает раскрытие способностей, даже приобретение дара, коего ранее не наблюдалось. Оттачивание мастерства вызовет развитие творческого начала, возрастание работоспособности и умственной активности. Дело само подведет к тропе преуспевания.
Единица из парочки напрямую покровительствует первенству человека, его превосходству над обществом. Следовательно, дарует заслуженное лидерство. Семёрка отвечает за активное проявление заложенных в личности талантов, врождённого дара, выливающегося в творчество и искусство.
Что обозначает поступках
В повседневных ситуациях знаменует необходимость воспитания самоуверенности и доверия к пространству.
Ситуативные советы и рекомендации:
Знак со сдвоенной 17 сообщает, что меняться нормально для человека. Опыт делает вас мудрее. А за ним приходит переоценка текущих приоритетов. Не застывайте в устаревших взглядах. Меняйтесь.
Духовные подсказки карт Таро
В колоде под номером семнадцать идет старший аркан Звезда — символ достижимого благополучия, молодости, энергии и надежды. Трактовки:
Увидевшему повторяющуюся 17 надо научиться надеяться на себя и небесных защитников. Здесь требуется баланс. Работайте, добивайтесь, но не забывайте об ангельском внимании к собственной персоне. Дайте им тоже потрудиться, регулярными просьбами о том, чего пока сами получить не в состоянии.
Деление чисел с остатком
Деление с остатком целых положительных чисел
Деление — это разбиение целого на равные части.
Остаток от деления — это число, которое образуется при делении с остатком. То есть то, что «влезло» и осталось, как хвостик.
Чтобы научиться делить числа с остатком, нужно усвоить некоторые правила. Начнем!
Все целые положительные числа являются натуральными. Поэтому деление целых чисел выполняется по всем правилам деления с остатком натуральных чисел.
Попрактикуемся в решении.
Пример
Разделить 14671 на 54.
Выполним деление столбиком:
Неполное частное равно 271, остаток — 37.
Ответ: 14671 : 54 = 271(остаток 37).
Деление с остатком положительного числа на целое отрицательное
Чтобы легко выполнить деление с остатком положительного числа на целое отрицательное, обратимся к правилу:
В результате деления целого положительного a на целое отрицательное b получаем число, которое противоположно результату от деления модулей чисел a на b. Тогда остаток равен остатку при делении |a| на |b|.
Неполное частное — это результат деления с остатком. Обычно в ответе записывают целое число и рядом остаток в скобках.
Это правило можно описать проще: делим два числа со знаком «плюс», а после подставляем «минус».
Все это значит, что «хвостик», который у нас остается, когда делим положительное число на отрицательное — всегда положительное число.
Алгоритм деления положительного числа на целое отрицательное (с остатком):
Пример
Разделить 17 на −5 с остатком.
Применим алгоритм деления с остатком целого положительного числа на целое отрицательное.
Разделим 17 на − 5 по модулю. Отсюда получим, что неполное частное равно 3, а остаток равен 2. Получим, что искомое число от деления 17 на − 5 = − 3 с остатком 2.
Ответ: 17 : (− 5) = −3 (остаток 2).
Деление с остатком целого отрицательного числа на целое положительное
Чтобы быстро разделить с остатком целое отрицательное число на целое положительное, тоже придумали правило:
Чтобы получить неполное частное с при делении целого отрицательного a на положительное b, нужно применить противоположное данному числу и вычесть из него 1. Тогда остаток d будет вычисляться по формуле:
d = a − b * c
Из правила делаем вывод, что при делении получается целое неотрицательное число.
Для точности решения применим алгоритм деления а на b с остатком:
Рассмотрим пример, где можно применить алгоритм.
Пример
Найти неполное частное и остаток от деления −17 на 5.
Разделим заданные числа по модулю.
Получаем, что при делении частное равно 3, а остаток 2.
Так как получили 3, противоположное ему −3.
Необходимо отнять единицу: −3 − 1 = −4.
Чтобы вычислить остаток, необходимо a = −17, b = 5, c = −4, тогда:
d = a − b * c = −17 − 5 * (−4) = −17 − (− 20) = −17 + 20 = 3.
Значит, неполным частным от деления является число −4 с остатком 3.
Ответ: (−17) : 5 = −4 (остаток 3).
Деление с остатком целых отрицательных чисел
Сформулируем правило деления с остатком целых отрицательных чисел:
Для получения неполного частного с от деления целого отрицательного числа a на целое отрицательное b, нужно произвести вычисления по модулю, после чего прибавить 1. Тогда можно произвести вычисления по формуле:
d = a − b * c
Из правила следует, что неполное частное от деления целых отрицательных чисел — положительное число.
Алгоритм деления с остатком целых отрицательных чисел:
Пример
Найти неполное частное и остаток при делении −17 на −5.
Применим алгоритм для деления с остатком.
Разделим числа по модулю. Получим, что неполное частное равно 3, а остаток равен 2.
Сложим неполное частное и 1: 3 + 1 = 4. Из этого следует, что неполное частное от деления заданных чисел равно 4.
Для вычисления остатка применим формулу. По условию a = −17, b = −5, c = 4, тогда получим d = a − b * c = −17 − (−5) * 4 = −17 − (−20) = −17 + 20 = 3.
Получилось, что остаток равен 3, а неполное частное равно 4.
Ответ: (−17) : (−5) = 4 (остаток 3).
Деление с остатком с помощью числового луча
Деление с остатком можно выполнить и на числовом луче.
Пример 1
Рассмотрим выражение: 10 : 3.
Отметим на числовом луче отрезки по 3 деления. Видим, что три деления помещаются полностью три раза и одно деление осталось.
Решение: 10 : 3 = 3 (остаток 1).
Пример 2
Рассмотрим выражение: 11 : 3.
Отметим на числовом луче отрезки по 3 деления. Видим, что три деления поместились три раза и два деления осталось.
Решение: 11 : 3 = 3 (остаток 2).
Проверка деления с остатком
Пока решаешь пример, бывает всякое: то в окно отвлекся, то друг позвонил. Чтобы убедиться в том, что все правильно, важно себя проверять. Особенно ученикам 5 класса, которые только начали проходить эту тему.
Формула деления с остатком
a = b * c + d,
где a — делимое, b — делитель, c — неполное частное, d — остаток.
Эту формулу можно использовать для проверки деления с остатком.
Пример
Рассмотрим выражение: 15 : 2 = 7 (остаток 1).
В этом выражении: 15 — это делимое, 2 — делитель, 7 — неполное частное, а 1 — остаток.
Чтобы убедиться в правильности ответа, нужно неполное частное умножить на делитель (или наоборот) и к полученному произведению прибавить остаток. Если в результате получится число, которое равно делимому, то деление с остатком выполнено верно. Вот так:
Теорема о делимости целых чисел с остатком
Если нам известно, что а — это делимое, тогда b — это делитель, с — неполное частное, d — остаток. И они между собой связаны. Эту связь можно описать через теорему о делимости с остатком и показать при помощи равенства.
Теорема
Любое целое число может быть представлено только через целое и отличное от нуля число b таким образом:
где q и r — это некоторые целые числа. При этом 0 ≤ r ≤ b.
Доказательство:
Если существуют два числа a и b, причем a делится на b без остатка, тогда из определения следует, что есть число q, и будет верно равенство a = b * q. Тогда равенство можно считать верным: a = b * q + r при r = 0.
Тогда необходимо взять q такое, чтобы данное неравенством b * q
Область допустимых значений функции
Допустимые и недопустимые значения переменных
В 7 классе заканчивается математика и начинается ее-величество-алгебра. Первым делом школьники изучают выражения с переменными.
Мы уже знаем, что математика состоит из выражений — буквенных и числовых. Каждому выражению, в котором есть переменная, соответствует область допустимых значений (ОДЗ). Если игнорировать ОДЗ, то в результате решения можно получить неверный ответ. Получается, чтобы быстро получить верный ответ, нужно всегда учитывать область допустимых значений.
Чтобы дать верное определение области допустимых значений, разберемся, что такое допустимые и недопустимые значения переменной.
Рассмотрим все необходимые определения, связанные с допустимыми и недопустимыми значениями переменной.
Выражение с переменными — это буквенное выражение, в котором буквы обозначают величины, принимающие различные значения.
Значение числового выражения — это число, которое получается после выполнения всех действий в числовом выражении.
Выражение с переменными имеет смысл при данных значениях переменных, если при этих значениях переменных можно вычислить его значение.
Выражение с переменными не имеет смысла при данных значениях переменных, если при этих значениях переменных нельзя вычислить его значение.
Теперь, опираясь на данные определения, мы можем сформулировать, что такое допустимые и недопустимые значения переменной.
Допустимые значения переменных — это значения переменных, при которых выражение имеет смысл.
Если при переменных выражение не имеет смысла, то значения таких переменных называют недопустимыми.
В выражении может быть больше одной переменной, поэтому допустимых и недопустимых значений может быть больше одного.
Пример 1
Рассмотрим выражение 
В выражении три переменные (a, b, c).
Запишем значения переменных в виде: a = 1, b = 1, c = 2.
Такие значения переменных являются допустимыми, поскольку при подстановке этих значений в выражение, мы легко можем найти ответ: 
Таким же образом можем выяснить, какие значения переменных — недопустимые.
Подставим значения переменных в выражение 
На ноль делить нельзя.
Что такое ОДЗ
ОДЗ — это невидимый инструмент при решении любого выражении с переменной. Чаще всего, ОДЗ не отображают графически, но всегда «держат в уме».
Область допустимых значений (ОДЗ) — это множество всех допустимых значений переменных для данного выражения.
Пример 2
Рассмотрим выражение 
Пример 3
Рассмотрим выражение 
ОДЗ такого выражения будет выглядеть вот так: b ≠ c; a — любое число.
Такая запись означает, что область допустимых значений переменных b, c и a = это все значения переменных, при которых соблюдаются условия b ≠ c; a — любое число.
Как найти ОДЗ: примеры решения
Найти ОДЗ — это значит, что нужно указать все допустимые значения переменных для выражения. Часто, чтобы найти ОДЗ, нужно выполнить преобразование выражения.
Чтобы быстро и верно определять ОДЗ, запомните условия, при которых значение выражения не может быть найдено.
Мы не можем вычислить значение выражения, если:
Теперь, приступая к поиску ОДЗ, вы можете сверять выражение по всем этим пунктам.
Давайте потренируемся находить ОДЗ.
Пример 4
Найдем область допустимых значений переменной выражения a 3 + 4 * a * b − 6.
В куб возводится любое число. Ограничений при вычитании и сложении нет. Это значит, что мы можем вычислить значение выражения a 3 + 4 * a * b − 6 при любых значениях переменной.
ОДЗ переменных a и b — это множество таких пар допустимых значений (a, b), где a — любое число и b — любое число.
Ответ: (a и b), где a — любое число и b — любое число.
Пример 5
Найдем область допустимых значений (ОДЗ) переменной выражения 
Здесь нужно обратить внимание на наличие нуля в знаменатели дроби. Одним из условий, при котором вычисление значения выражения невозможно явлется наличие деления на ноль.
Это значит, что мы может сказать, что ОДЗ переменной a в выражении 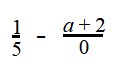— пустое множество.
Пустое множество изображается в виде вот такого символа Ø.
Пример 6
Найдем область допустимых значений (ОДЗ) переменных в выражении 
Если есть квадратный корень, то нам нужно следить за тем, чтобы под знаком корня не было отрицательного числа. Это значит, что при подстановке значений a и b должны быть условия, при которых a + 3 * b + 5 ≥ 0.
Ответ: ОДЗ переменных a и b — это множество всех пар, при которых a + 3 * b + 5 ≥ 0.
Пример 7
Найдем ОДЗ переменной a в выражении 
Прежде всего, нам нужно подобрать такое условие, при котором в знаменателе дроби не будет ноля — 
Мы знаем, что выражение под знаком корня должно быть положительным. Это дает нам второе условие: a + 1 ≥ 0.
Мы не можем вычислить логарифм отрицательного выражения. Получаем третье условие: a 2 + 2 > 0.
Выражении в основании логарифма не должно быть отрицательным и не должно равняться единице. Получаем условие 4: a + 6 > 0.
Как видите, записывая ОДЗ, мы ставим квадратные и круглые скобки.
Запомните
Например, если х > 6, но х
Зачем учитывать ОДЗ при преобразовании выражения
Иногда выражение просто невозможно решить, если не выполнить ряд тождественных преобразований. К ним относятся: перестановки, раскрытие скобок, группировка, вынесение общего множителя за скобки, приведение подобных слагаемых.
Кроме того, что видов таких преобразований довольно много: нужно понимать, в каких случаях какое преобразование возможно. В этом может помочь определение ОДЗ.
Тождественное преобразование может:
Рассмотрим каждый случай в отдельности.
Пример 8
Поскольку мы должны следить за тем, чтобы в выражении не возникало деление ноль, определяем условие a ≠ 0.
Это условие отвечает множеству (−∞ ; 0) ∪ (0 ; +∞).
В выражении есть подобные слагаемые, если привести подобные слагаемые, то мы получаем выражение вида a.
ОДЗ для a — это R — множество всех вещественных чисел.
Преобразование расширило ОДЗ — добавился ноль.
Пример 9
Рассмотрим выражение a 2 + a + 4 * a
ОДЗ a для этого выражения — множество R.
В выражении есть подобные слагаемые, выполним тождественное преобразование.
После приведения подобных слагаемых выражение приняло вид a 2 + 5 * a
ОДЗ переменной a для этого выражения — множество R.
Это значит, что тождественное преобразование никак не повлияло на ОДЗ.
Пример 10
Рассмотрим выражение 
Решить такое неравенство можно методом интервалов, что дает нам ОДЗ (−∞; 1] ∪ [4 ; +∞).
Затем выполним преобразование исходного выражения по свойству корней: корень произведения = произведению корней.
Приведем выражение к виду 
Решив систему линейных неравенств, получаем множество [4; + ∞).
Отсюда видно, что тождественные преобразования сузили ОДЗ.
От (−∞; 1] ∪ [4 ; +∞) до [4; + ∞).
Решив преобразовать выражение, внимательно следите за тем, чтобы не допустить сужение ОДЗ.
Запомните, что выполняя преобразование, следует выбирать такие, которые не изменят ОДЗ.